
Für Anfänger
gibt es eine Einführung in die Thematik des kosmischen Plasmas unterstützt durch Youtube MoviesDer Leitfaden
der Elektro- dynamik ist die Voraussetzungen, um die Eigen- schaften des Plasmas, des Aggregatzustandes, in dem sich der Kosmos zu mehr als 99% befindet, zu verstehen..Missverständnisse
sind der Grund, warum viele Leute die Ideen des Elektrischen Universums ablehnen. Hier wird mit den Missverständnissen aufgeräumt.





Vom Mysterium der
Schöpfung zur Kernfusion
Die Vajra ist das Symbol des Thunderbolt ProjektsSpaceNews
In Kurzfilmen mit deutschen Untertiteln werden die neuesten Erkenntnisse über den Kosmos dargestellt.immer aktuell
unterstützt von
mugglebibliothek.de



Wer Interesse an der Unterstützung
dieser Website hat, melde sich
bitte bei
jasta72s@gmail.com
Willkommen bei einer
Stimme für das
Elektrische Universum
l
etzte Änderung: 11.12.2021
Unsere Vorstellung von der Sonne
Ein Widerspruch zwischen Theorie und technischem Modell
von Mathias Hüfner am 8. Oktober 2015 aktualisiert am 5. November 2015 Das Standardmodell der Sonne behauptet, dass die Sonne ein langsam brennender thermonukleare Ofen sei, in dessen Inneren eine Temperatur von ca. 15.6 Millionen Kelvin herrschen würde, ähnlich einer Wasserstoffbombe, nur gesteuert. Doch außer dieser Idee hat das Standardmodell der Sonne nichts mit der technischen Realisierung dieser Idee zu tun. Hier trennen Ingenieure und Astrophysiker Welten. Während technische Nachbauten von kosmischen Vorgängen Maschinen erfordern, die Unmengen an Elektrizität benötigen, ignorieren Astrophysiker bis heute strikt die Bedeutung von Elektrizität für die Bildung kosmischer Strukturen und bevorzugen stattdessen die um viele Größenordnungen schwächere Gravitation für die Erklärungsversuche ihres Weltverständnisses. Was noch 2006 gelehrt wurde, zeigt eine Seminararbeit an der RWTH Achen zum Neutrinoproblem der Sonne. Das Neutrinoproblem wurde als das Hauptproblem für die Anerkennung des auf Konvektion beruhenden thermonuklearen Sonnenmodells angesehen. Es stellte sich heraus, dass man nur etwa die Hälfte der erwarteten Neutrinos fand. Die Anzahl der von der Sonne kommenden Neutrinos war das über dreißig Jahre ungelöste Problem für das Sonnenmodell der Astrophysiker. Um das thermonukleare Modell zu retten, erfand man die Neutrinooszillation Nun soll dieses Problem dadurch wegdiskutiert werden, indem man behauptet, dass sich die Neutrinos in eine andere Neutrinoart durch Wechselwirkung mit der Materie umgewandelt hätten, die deshalb nicht nachweisbar gewesen wären. Das hätte man experimentell festgestellt. Das Experiment ist nur leider nicht nachvollziehbar. Außerdem bleibt die Frage, warum sollen sich Neutrinos eine andere Gestalt zulegen, die sie für bestimmte Detektoren unsichtbar macht? Angeblich wechselwirken Neutrinos mit ihrer Umgebung doch kaum, nun aber doch? Das alles ist einem klaren Verstand nur schwer zu vermitteln.Vergleich des Konvektionsmodells mit der technischen Modellierung des Fusionsprozesses
Schauen wir uns nun einmal an, wie weit Ingenieure mit dem Sonnenmodell gekommen sind. Im Gegensatz zu Astrophysikern, die sich mit einer Theorie zufrieden geben, der keiner mehr widerspricht oder widersprechen darf, gibt sich der Ingenieur erst zufrieden, wenn er das Prinzip durch eine Apparatur nachgebaut hat. Analysiert man das Problem der Wasserstoffbombe, stellt man fest, dass es schwer wird, die Reaktionspartner im Inneren einer Masse zusammen zuhalten. Das soll die Gravitation bewirken, obwohl dazu im Labor starke Elektromagneten nötig sind. Auf der Erde sehen wir, dass jedes Feuer die Massen gegen die Schwerkraft verteilt und nur die schweren Bestandteile als Asche zurückbleiben. Notwendige Temperaturen von 30 Millionen bis 100 Millionen Grad ergeben nach dem Energiesatz Geschwindigkeiten zwischen 720km/s und 1300km/s für die einzelnen Protonen. Es ergibt sich jedoch die Frage, wie in einem dichten Medium, wie es im Inneren der Sonne auf Grund ihrer Größe existiert, sich solche Geschwindigkeiten unter thermischen Bedingungen entwickeln können, Entweder das Medium explodiert oder die Temperaturen bleiben eher moderat. Es ist unwahrscheinlich, dass im Inneren der Sonne um mehrere Größenordnungen höhere Temperaturen als an ihrer Oberfläche herrschen. Die Oberflächentemperatur der Sonne wird durch die Farbtemperatur der Sonnenflecken gegeben. Die liegt etwa bei 4000K. Die Photosphäre darüber hat bereits eine Temperatur von mehr als 5500K. Das kann man sich etwa so erklären, dass die Flamme einer Kerze am Docht auch kälter als an ihrer Spitze ist. Also werden diese hohen Temperaturen eher in der Photosphäre zu erwarten sein. Um die Reaktionspartner für eine dauerhafte Fusion zusammenzuhalten, ist ein starkes Magnetfeld notwendig. Dazu wird aber Elektrizität benötigt. In einem Brief an Einstein , datiert vom 26.August 1951, schrieb der junge Student Ernest Sternglass, “ Es könnte Sie interessierten zu erfahren, dass ich seit den letzten zwei Monaten nun ich in der Lage bin, experimentelle Belege für die Bildung von Neutronen aus Protonen und Elektronen in einer Hochspannungsentladung von Wasserstoff zu erhalten. ” Das erkannte man auch 1952 in Moskau, als von den sowjetischen Physikern Andrei Sacharow (dem Vater der dortigen Wasserstoffbombe) und Igor Jewgenjewitsch Tamm am Kurtschatow-Institut[1] das Tokamak-Prinzip entwickelt wurde. Das Wort ist eine Transliteration des russischen токамак, eine Abkürzung für „тороидальная камера в магнитных катушках“ ( 'tɔraidalʲnaia kamʲɛra v magnitnɨx katuʃkax ), übersetzt Toroidale Kammer in Magnetspulen. Auch verweist die Silbe ток auf Strom und damit den Stromfluss im Plasma, die entscheidende Besonderheit dieses Einschlusskonzepts. Die Reaktionspartner sollen in einem Thorus auf die notwendige Reaktionsgeschwindigkeit gebracht werden, wie auch in seinem großen Bruder dem LHC . Nur fehlen am Tokamak die Detektoren. Damit sich keine Wirbel zwischen den in der Mitte schneller kreisenden Deuteriumkernen (einem schweren Wasserstoffisotop) und den an den Rändern langsamer kreisenden Kerne bilden, ist ein Stromfluss notwendig, um alle Ionen auf einer spiralförmigen Bahn zu halten. Das wird durch einen großen Transformator bewerkstelligt. Dieser stellt gleichzeitig eine Ohm’sche Heizung für das Plasma im Thorus dar. Da man nicht ständig den Stromfluss in den Magnetspulen steigern kann, muss dieser von Zeit zu Zeit abgeschaltet werden. Hierdurch geht der Plasmaeinschluss verloren und die Kernfusion kommt zum Erliegen. Am 9. November 1991 konnte am Joint European Torus JET erstmals eine nennenswerte Energiemenge aus kontrollierter Kernfusion freigesetzt werden. Ein Deuterium-Tritium-Plasma lieferte zwei Sekunden lang eine Leistung von 1,8 Megawatt. 1997 wurde eine Fusionsleistung von 16 Megawatt erreicht, wobei allerdings 24 Megawatt für die Plasmaheizung erforderlich waren. Jedoch verbrauchten die Umwälzpumpen mehr Energie als durch Kernfusion frei wurde. Dieses Prinzip hat den Nachteil, dass es nur im Pulsmodus arbeitet. Es gibt ein weiteres Prinzip, den Stellarator. Bei diesem erfolgt der Einschluss eines Plasmas in einer ringförmigen (torusförmigen) Anlage durch spiralförmige Überlagerung von Magnetfeldern. Das geschieht mittels Magnetfeldspulen, die selbst bereits so wie ein Möbiusband verdrillt sind, so dass auch der im Querschnitt des Ringes wirksame Anteil des Feldes durch die Spulen erzeugt wird, anstatt durch einen im Plasma induzierten Strom wie beim Tokamak. Ein Stellarator benötigt somit keinen im Plasma fließenden Strom, der im klassischen Tokamak in der Art eines Transformators erzeugt wird, und ist daher im Unterschied zum gepulsten Betrieb eines Tokamaks unmittelbar für den Dauerbetrieb geeignet. Wegen der komplexeren Spulen sind Konstruktion und Fertigung sowie Wartungs- und Reparaturarbeiten jedoch aufwendiger. Eine Optimierung der Spulengeometrie dank leistungsfähiger Computerprogramme und die Fertigung solcher Spulen gelangen erst in jüngerer Zeit; dadurch weist die Tokamak-Entwicklung einen zeitlichen Vorsprung auf. Mit Wendelstein 7-X wird im nordostdeutschen Greifswald aktuell erstmals ein großer Stellarator mit einer solchen optimierten Spulengeometrie aufgebaut, um das Stellarator-Konzept auf seine Eignung für einen Fusionsreaktor zu untersuchen. Ein weiterer wichtiger Gesichtspunkt eines akzeptierbaren Sonnenmodells ist die Frage nach der Zuführung des Brennstoffes, um den Prozess am Laufen zu erhalten. Wenn der Brennstoff uneingeschränkt zur Verfügung steht, ist die Folge eine Explosion wie bei einer Wasserstoffbombe. Es muss also eine gesteuerte Zufuhr dieses Brennstoffes erfolgen. Wenn dieser Brennstoff im Inneren der Sonne lagern soll, ist doch die Frage, was verhindert, dass es zu einer Explosion kommt, bzw. was löst eine Supernova aus? Letzteres soll passieren, wenn der Brennstoff verbraucht ist und es gäbe zwei grundsätzliche Mechanismen, nach denen Sterne zur Supernova werden können: 1 . Massereiche Sterne mit einer Anfangsmasse von mehr als etwa acht Sonnenmassen , deren Kern am Ende ihrer Entwicklung und nach Verbrauch ihres nuklearen Brennstoffs kollabiert. Hierbei könne ein kompaktes Objekt, etwa ein Pulsar oder ein hypothetisches „Schwarzes Loch“ entstehen. 2 . Sterne mit geringerer Masse von einer angenommenen Größe von etwa einem Hundertstel des Sonnendurchmessers, die als Weißer Zwerg Material aufsammeln sollen, und dann durch Eigengravitation kollabieren(!) würden und dabei durch einsetzendes Kohlenstoffbrennen zerrissen würden. Fusion Ja - Konvektion Nein Beide Erklärungen der Explosion von Sternen sind aus energetischen Gründen unlogisch. Eine Explosion ist eine Freisetzung von Energie, bei der ein Massevolumen sich schlagartig auf das Vielfache seines ursprünglichen Volumens ausdehnt. Dieser Prozess wird durch eine geringe Energiezufuhr von Außen ausgelöst, wenn sich die Masse in einem für die Energiezufuhr kritischen Zustand befindet. Es muss sich also explosiver Sprengstoff angehäuft haben und es muss Energie von außen zugeführt werden, damit es zu einer Explosion kommt. Schauen wir uns die Kernprozesse in der Sonne näher an. Die sogenannte Proton-Proton-Reaktion soll die erste Fusionsreaktion sein, die in der Sonne bei Temperaturen von 4 Millionen Kelvin zuerst zündet und mit 98.4% den überragenden Beitrag zur solaren Energieerzeugung liefern soll. Zunächst fusionieren zwei Wasserstoffkerne 1 H (Protonen) zu einem Deuteriumkern 2 D , wobei durch die Umwandlung eines Protons in ein Neutron, ein Positron e + und ein Elektronneutrino ν e frei werden. 1 H + 1 H → 2 D + e + + ν e + 0,42 MeV (1) Die Reaktionsrate ist offensichtlich kleiner als die der Folgereaktionen und damit für die Gesamtreaktion geschwindigkeits-bestimmend. Grund ist, dass die elektrostatische Abstoßung die positiv geladenen Protonen meist auf Abstand hält und die Entstehung des Neutrons als Prozess der schwachen Wechselwirkung nur bei sehr kleinen Abständen möglich ist. Von der relativ geringen Energiefreisetzung der Reaktion trägt das Neutrino durchschnittlich 0,26 MeV davon. Da diese leichten Teilchen die Sternmaterie nahezu ungehindert durchdringen, ist dieser Energieanteil für die Sternphysik verloren. Das entstandene Positron annihiliert sofort mit einem Elektron , d.h., sie reagieren miteinander und werden vollständig in Energie umgewandelt. Die Masse beider Partner wird in Form von zwei Gammaquanten γ als Energie von je 511keV frei. e + + e− → 2γ + 1,022 MeV (2) Da auch ein Elektron in dem Prozess vernichtet wird, bleibt das positive Potential erhalten, weil nun an anderer Stelle ein Elektron fehlt. Das bewirkt einen Stromfluss. Diese Ereignisse können jedoch zu großen Schwankungen in der Abstrahlung von γ -Strahlen führen und es bedeutet auch, dass sich das ursprüngliche Ladungsgleichgewicht mit zunehmender Dauer des Fusionsprozesses zu einer positiven Ladung der Sonne verschieben muss. Die Sonne wird zu einer Anode. Das entstandene Deuterium kann anschließend mit einem weiteren Proton reagieren, wobei das leichte Helium- Isotop 3 He entsteht:. 2 D + 1 H → 3 He + g + 5,49 MeV (3) Abbildung 1 Tokamak -Prinzip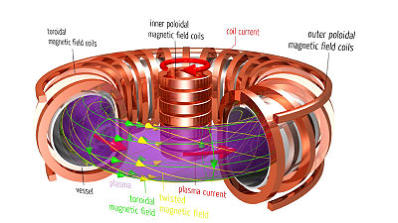
Anschließend
erfolgen
weitere
Reaktionen,
in
denen
4
He
und
weitere
Elemente
entstehen.
Siehe
Abbildung
3.
Einen
weiteren
Zyklus
bezeichnet
man
als
den
CNO-
oder
Bethe-Weizsäcker-Zyklus.
In
diesem
Zyklus
entstehen
weitere Positronen, was das positive Potential weiter erhöht.
Die
Energiegewinne
wurden
aus
den
Massendefiziten
zwischen
Ausgangs-
und
Endprodukt
berechnet.
Nicht
aufgeführt
sind
die
Energien,
um
die
Reaktion
zu
starten.
In
der
Praxis
ist
immerhin
eine
Atombombe
notwendig,
um
eine
Wasserstoffbombe
zu
zünden.
Es
müssen
zwei
positive
Ladungen
so
nahe
gebracht
werden,
dass
ein
Proton
sich
in
ein
Neutron
verwandelt.
Dazu
ist
eine
Kraft
notwendig,
die
die
Gravitation
zwischen
zwei
Wasserstoffatomen
um 39 Größenordnungen übersteigt. Nach der klassischen Maxwell-Boltzmann-Gleichung
kann
man
den
Energiebedarf
für
die
obigen
Fusionsgleichungen
abschätzen,
wenn
man
die
Zündtemperaturen
kennt.
Bei
einer
Zündtemperatur
von
30
Millionen
Kelvin
ergibt
sich
ein
Energieaufwand
für
die
Gleichung
(1)
von
ca.
-4keV.
Das
erscheint
auf
den
ersten
Blick
gegenüber
dem
Energiegewinn
vernachlässigbar.
Damit
allerdings
eine
Kollision
möglich
wird,
müssen
die
Protonen
sich
in
elektrischen
Feldern
auf
Kollisionskurs
befinden
können.
Das
dürfte
bei
thermischer
Aufheizung
kaum
gelingen.
Tatsächlich
registriert
man
aber
kurzzeitige
Gamma-Ausbrüche
ständig überall im Kosmos.
Der
umgekehrte
Fall,
die
Verwandlung
von
freien
Neutronen
in
Protonen
und
Elektronen
hat
eine
Halbwertszeit
von
12
min,
was
bedeutet,
dass
freie
Neutronen
auf
der
Sonne
kaum
zu
finden
sein
werden.
Bei
der
Explosion
einer
Atombombe
entstehen
dagegen
schlagartig
jede
Menge
freier
Neutronen,
die
in
einem
dichten
verwirbelten
Plasma
anschließend die Wasserstoff-Fusion zünden können.
Vergleicht
man
das
mit
dem
technischen
Sonnenmodell,
so
muss
man
feststellen,
dass
der
Brennstoff
im
Tokamak
aus
Deuterium
und
Tritium
besteht,
-
also
Isotopen
von
Wasserstoff,
die
die
Neutronen
bereits
mitbringen
-
Isotope,
die
in
der
natürlichen
Umwelt
recht
selten
anzutreffen
sind.
Warum
treibt
man
dann
solchen
Aufwand,
um
an
die
wesentlich
selteneren
Isotope
des
Wasserstoffs
zu
kommen,
wenn
man
sie
doch
im
Prozess
erzeugen
könnte?
Offensichtlich,
weil
es
unter
Laborbedingungen
nicht
möglich
ist,
die
nötige
Zündenergie
in
einem
genügend
dichten
Plasma
dafür
aufzubringen,
bzw.
diese
über
einen
längeren
Zeitraum
aufrecht
zu
erhalten.
Damit
der
Prozess
der
Sonne
am
Laufen
gehalten
werden
kann,
muss
es
offensichtlich
in
ihrer
Atmosphäre
eine
Neutronenquelle
bzw.
einen
Prozess
geben,
der
gerade
so
viele
Neutronen
ständig
nachliefert,
dass
das
atomare
Feuer
am
Laufen
gehalten
wird.
Das
könnte
beispielsweise
durch
die
Beschleunigung
von
Protonen
im
elektrischen
Feld
der
Photosphäre
passieren,
die
mit
anderen
Protonen
in
den
Turbulenzen
der
Korona
kollidieren.
[Siehe:
Scott
]
David
Talbott,
der
das
Fusionsmodell
im
obigen
Aufsatz
in
Frage
stellt
und
gleichzeitig
gegen
das
technische
Konzept
des
Fusionsreaktors
polemisiert,
bietet
in
seinem
Beitrag
eine
Menge
Anregungen,
die
es
wert
sind,
durchdacht
zu
werden,
wie
zum
Beispiel
der
Hinweis
auf
die
abrupte
Temperatur-steigerung
in
der
Sonnenkorona
mit
einer
Temperaturerhöhung
bis
auf
200
Millionen
Grad
Kelvin
für
ionisierten
Sauerstoff
in
einem
Abstand
von
1
bis
2
Sonnendurchmessern!
Sauerstoff
steht
nämlich
am
Ende
der
Fusionskette
des
Bethe-Weizsäcker-Zyklus
.
Der
Bethe-
Weizsäcker-Zyklus
läuft
erst
bei
Temperaturen
über
14
Millionen
Grad
Kelvin
ab
und
soll
ab
30
Millionen
Grad
Kelvin
vorherrschend
sein.
Aus
optischen
Spektren
von
aktiven
Galaxien
sind
die
Elemente
Stickstoff-
und
Sauerstoff-Ionen
als
starke
Spektrallinien
zu
beobachten,
was
als
Hinweis
auf
den
CNO-
Zyklus
gewertet
werden
kann.
In
der
neben
stehenden
Abbildung
4
ist
die
Menge
der
Elemente
O+++
und
N++
ausgedrückt
durch
die
Äquivalenzbreite
der
Spektrallinien
im
Verhältnis
zu
Wasserstoff,
repräsentiert
durch
die
H
a
-
Line,
im
logarith-mischen
Maßstab
dargestellt.
Dabei
stellt
jede
Galaxie
einen
Punkt
dar.
Interessant
ist,
dass
sich
die
Punktwolke
halbmondförmig
um
die
Linien
x=2
→¨
Wasserwelten
und
y=3
→¨
Amoniakwelten
gruppiert.
Da
diese
Elemente
in
den
Spektren
sichtbar
sind,
können
die
Fusionsprozesse
nicht
im
Inneren
der
Sonne
ablaufen,
sondern müssen in deren Atmosphären ablaufen.
Es
sind
noch
viele
Fragen
zu
klären,
bis
wir
die
Prozesse
auf
der
Sonnen
völlig
verstanden
haben.
Sie
werden
wohl
nicht
zu
verstehen
sein,
wenn
wir
die
Wechselwirkung
der
Sonne
mit
ihrer
Umgebung
nicht
berücksichtigen.
Mit
einer
Umgebung,
die
alles
andere
als
ein
Vakuum
ohne
jegliche
Funktion
ist,
die
wir
bisher
nicht
berücksichtigt
haben,
weil
sie
für
unser
menschliches
Auge
unsichtbar
blieb,
die
aber
in
der
über-wiegenden
Menge
aus
Plasmaströmen
von
Wasserstoff
besteht,
wie
aus
Beobachtungen
anderer
Galaxien
zu
entnehmen
ist.
Sollten
nicht
die
kontinuierlich
von
außen
zugeführten
Ströme
dafür
sorgen,
dass
der
Fusionsprozess
nicht
in
einer
einzigen
Explosion
endet?
Man
muss
die
Idee
des
Fusionsmodell
nicht
grundsätzlich
in
Frage
stellen,
aber
man
muss
sich
von
liebgewordenen
Vorstellungen
verabschieden,
wie
und
wo
diese
Fusion
ablaufen
soll,
ob
im
Inneren
der
Sonne
oder in ihrer aufgeheizten Photosphäre, ob mit oder ohne Beteiligung von intergalaktischen Plasmaströmen.
Abschätzung des notwendigen Elektronenstroms für die Sonne
Aus den obigen Formeln (1),(2) und (3) erhalten wir eine von der Sonne freigesetzt Energie von 6,932MeV / Fusion, wobei jeweils ein positive Ladung entsteht. Das ergibt 1,11×10e-12 Wattsekunde [Ws]. Daraus lässt sich die Fusionsleistung der Sonne an der Oberfläche berechnen. Die Sonnenoberfläche gibt 6,5×10e+7 W/m² Leistung ab. Indem wir diese Leistung durch die Leistungsabgabe einer Fusion teilen, erhalten wir die Anzahl der Fusionen pro Sekunde und m² . → 6,5×10e+7 / 1,11×10e-12 Fusionen /m²s = 5,8× 10e+19 Fusionen/m²s unter der Voraussetzung, dass Kernfusion der pp-Kette die einzige Energiequelle ist. Das ergibt auch die Anzahl der positiven Ladungen pro Quadratmeter und Sekunde auf der Sonne. Die Sonnenoberfläche beträgt etwa 6× 10e+18 m² . → 5,8×10e+19 Fusionen/m²s × 6×10e+18 m² = 3,48×10e+38 Fusionen/s auf der gesamten Sonnenoberfläche Die verbrauchen 3,48×10e+38 Elektronen/s und erzeugen folglich die gleiche Zahl Protonen. Das ergibt 3,48×10e+38 × 1,11×10e-12 W = 3,9 ×10e+26 W . Nach Scott beträgt die Sonnenspannung 500kV. Indem man die Leistung durch die Spannung teilt, erhält man eine Stromstärke von 7,8 × 10e+20 A auf der Sonnenoberfläche . Im Aufsatz von Scott haben wir erfahren, dass Voyager 1 10 Millionen Elektronen/m²s auf der Heliopause gesammelt hat. Das ergibt mit Ir = Nev → 1.6×10e-7 A/m²s bei einer Elektronengeschwindigkeit von 1000km/s. Der Radius der Heliopause beträgt etwa 1.8×10e+13m nach Scott, so muss die sphärische Grenze eine Sammelfläche von etwas mehr als 5×10e+27 Quadratmetern haben. Scott meint: “ Eine solche Fläche würde dann einen Strom von interstellaren Elektronen in der Stärke von ca. 1,6×10e-7 A/m² × 5×10e+27 m² = 8 × 10e+20 A in der Sekunde sammeln.“ Das ist eine Abweichung von 2,5% zum Anodenstrom der Sonne und eine gute Bestätigung für die nukleare Herkunft des Anodenstroms, da es zu einem geringen Prozentsatz noch weitere Fusionsreaktionen gibt, die hier nicht mit erfasst sind. Das SAFIRE-Projekt , das von einer kleinen Forschergruppe um Don Scott und Montgommery Childs seit 2016 betrieben wird, weckt die Hoffnung, eine Energiequelle ähnlich der Sonne zur Nutzung in der Zukunft zur Verfügung zu bekommen. Es konnten mikroskopisch kleine Spuren von Kernumwandlung in der Vakuum-Brennkammer und auf der Anode des Laborreaktors nachgewiesen werden und der Energiegewinn war erstmalig größer als die aufgewendete Energie. Allerdings müssen die Physiklehrbücher neu geschrieben werden, weil unsere Vorstellung vom Atomkern nicht mit den Experimenten übereinstimmen.Schlussfolgerung
Das Fusionsmodell ist von der Grundidee nicht zu verwerfen, sondern nur die Vorstellung, dass die Fusion im Inneren unter dem Gravitationsdruck stattfinden würde und die Energie durch Konvektion nach oben befördert würde. Die Fusion produziert ein positives elektrisches Potential und wirkt daher wie eine Stromquelle. Viele Sterne bzw. ganze Galaxien können deshalb zu Reihen- , Parallel- und Sternschaltungen im Weltall verknüpft sein. Das Licht zwischen den Sternen der Galaxien ist das Kathodenlicht.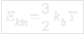


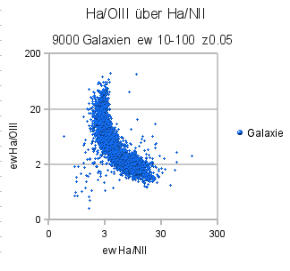







Abbildung 1. Das Tokamak-Prinzip Quelle: Wikipedia
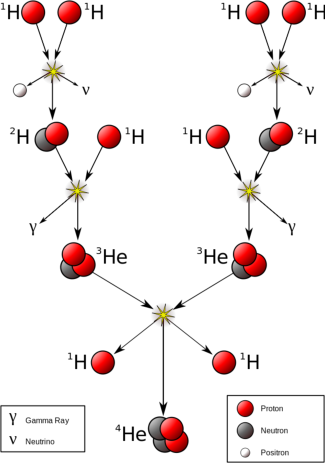
Abbildung2 Die p-p-Kette Quelle: Wikpedia
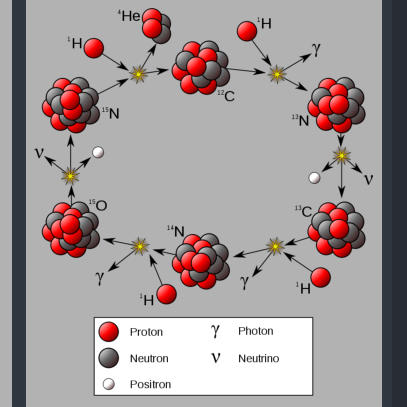
Abbildung3 Der Bethe-Weizsäcker-Zyklus
Quelle: Wikipedia
Abbildung 4. Verhältnis zwischen Wasser-
stoff und den Ionen von Sauerstoff und
Stickstoff in aktiven Galaxien
Quelle: M. Hüfner entnommen der
Datenbank Release 7 des Sloan Digital Sky
Survey-Projektes
Der solare Elektronenfluss
Der solare Elektronenfluss


- Vorwort
- Einführung
- 1. Abstände im Weltraum
- 2. Felder im Weltraum
- 3. Das Plasma
- 4. Der Elektromagnetismus
- 5. Stromfreie Doppelschichten u.a.
- 6. Ströme, Filamente und Pinche
- 7. Birkeland-Ströme und anderes
- 8. Stromschichen und -kreise
- 9. Instabilitäten
- 10. Rotationseffekte
- 11. Strahlung
- Elektrische Kometen
- Neues von Pluto
- Das Elektrische Sonnensystem
- Anhang1 - Vektoren
- Anhang2 - Maxwellsche Gleichung


- 1. Wo ist das Problem?
- 2. Wahre Wissenschaft
- 3. Wo bleibt die Mathematik?
- 4. Wo bleibt die Begutachtung?
- 5. Was ist mit der Gravitation?
- 6. Wie groß ist das Universum?
- 7. Wo ist der Leiter?
- 8. Ausbildungsdefizit?
- 9. Einstein widerlegt?
- 10. Warum Urknall bestreiten?
- 11. Was ist mit der Materie?
- 12. Elektrizität vor Magnetismus?















