
Für Anfänger
gibt es eine Einführung in die Thematik des kosmischen Plasmas unterstützt durch Youtube MoviesDer Leitfaden
der Elektro- dynamik ist die Voraussetzungen, um die Eigen- schaften des Plasmas, des Aggregatzustandes, in dem sich der Kosmos zu mehr als 99% befindet, zu verstehen..Missverständnisse
sind der Grund, warum viele Leute die Ideen des Elektrischen Universums ablehnen. Hier wird mit den Missverständnissen aufgeräumt.





Vom Mysterium der
Schöpfung zur Kernfusion
Die Vajra ist das Symbol des Thunderbolt ProjektsSpaceNews
In Kurzfilmen mit deutschen Untertiteln werden die neuesten Erkenntnisse über den Kosmos dargestellt.immer aktuell
unterstützt von
mugglebibliothek.de



Wer Interesse an der Unterstützung
dieser Website hat, melde sich
bitte bei
jasta72s@gmail.com
Willkommen bei einer
Stimme für das
Elektrische Universum
l
etzte Änderung: 11.12.2021
APPENDIX I
VEKTORALGEBRA
Vektorrechnung wird formuliert, um mit Vektoren umzugehen, d.h., Mengen mit einem Betrag und einer Richtung. Normale Algebra, Geometrie und Trigonometrie sind wirksam, wenn man mit skalaren Mengen arbeitet, das sind solche mit nur einem Betrag, die aber untauglich sind, wenn man mit Vektoren umgehen muss. Vektorrechnung ist ein wirksamer Weg, um 2D- und 3D-Probleme zu lösen, die Vektoren beinhalten, ohne unhandliche Geometrie zu gebrauchen. Das elektromagnetische (EM) Feld ist ein Vektorfeld von Kräften, die auf geladene Objekte einwirken. Da die Kräfte Vektormengen sind (Kräfte, die in eine verbundene Richtung wirken), beinhalten die EM-Feldgleichungen Vektoren. Vektoralgebra kann für kartesianische, zylindrische oder sphärische Koordinaten formuliert werden. Die geeignete Wahl eines Koordinatensystems für zylindrische oder sphärische symmetrische Probleme vermeidet das Aufkommen nutzloser Komplexität durch die Nutzung unangebrachter Koordinatensysteme und zeigt auch klar die Symmetrie der Lösung. Zwei wichtige Ergebnisse der Vektorrechnung beinhalten die Multiplikation der Vektoren. Vektoren werden durch fetten Text angezeigt. Das Punktprodukt (oder skalare Produkt) A ・ B (lies A punkt B) wird definiert als ||AB|| cos(θ) , wo A und B die Beträge (numerische Werte) bezüglich der Vektoren A und B sind und θ der Winkel zwischen ihnen ist. Man beachte, dass das Punktprodukt eine skalare Menge (ein einfacher numerischer Wert [Größe] ohne eine verbundene Richtung) ist und sich geometrisch in einer einzelnen Ebene (d.h. 2D) befindet. Wenn der Winkel zwischen den Vektoren > 90° ist, dann ist der Skalar negativ (<0). Wenn zwei Vektoren vertikal zueinander stehen, dann ist ihr Punktprodukt Null.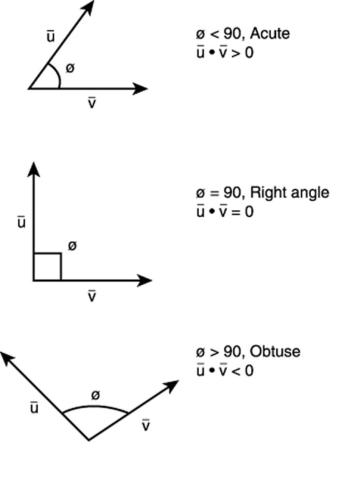
Courtesy Wiki Commons, Beschriftungen hinzugefügt

Übersetzung H. Täger
Anhang II - Maxwellsche Gleichungen
11. Strahlung




Anhang II - Maxwellsche Gleichungen
11. Strahlung



Beispiele für Skalarprodukte mit verschiedenen Winkeln
Das
Kreuzprodukt
A
×
B
(lies
“A
kreuz
B”)
ist
definiert
als
AB
sin(θ)
a
n
,
wo
a
n
der
Einheitsvektor
senkrecht
zu
der
Ebene
von
A
und
B
ist.
Man
beachte,
dass
das
Kreuzprodukt
von
zwei
Vektoren
auch
ein
Vektor
ist
und
seine
Richtung
orthogonal
(vertikal)
zu
beiden,
A
und
B
ist;
d.h.,
der
resultierende
Vektor
beinhaltet
eine
dritte
Dimension
im
Vergleich zu der 2D-Ebene, die die ersten zwei Vektoren enthält.
Die
Vektorrechnung
definiert
einen
anderen
wichtiger
Operator,
Del
,
oder
Δ.
Del
steht
für
den
Differentialoperator
D
in
der
Rechnung,
wobei
D
die
Operation
d/dx
vertritt.
Zwei
weitere
Ergebnisse,
die
D
nutzen,
sind wichtig beim Analysieren von EM-Feldern.
Δ
・
A
oder
div
A
ist
die
Divergenz
des
Vektorfeldes
A
.
Die
Divergenz
ist
ein
Skalar
und
ist
ähnlich
zu
der
Ableitung
einer
Funktion.
Wenn
die
Divergenz
einer
Region
eines
Vektorfeldes
nicht
Null
ist,
dann
wird
gesagt,
dass
die
Region
Quellen
(
div
A
>0)
oder
Ausgüsse
(
div
A
<0)
des
Feldes
enthält.
Zum
Beispiel:
Eine
willkürlich
um
eine
Oberfläche
geschlossene
Fläche
um
eine
isolierte
positive
Ladung
in
einem
statischen
elektrischen
Feld
enthält
die
Quelle
des
elektrischen
Flusses,
das
ist
die
positive
Punktladung;
deshalb
ist
die
Divergenz
des
elektrischen
Flussdichtevektorfeldes
über
dieser
Oberfläche
positiv
und
entspricht
der
eingeschlossenen
Ladung.
Das
ist
das
Gausssche Gesetz. (siehe
Anhang II, EM-Feldgleichungen
)
Man
beachte,
dass
div
A
ein
Punktprodukt
beinhaltet
und
deshalb
von
den
Winkeln
abhängt.
Der
Winkel
ist
gewöhnlich
der
zwischen
dem
analysierten
Vektor
und
der
Oberflächennormalen
[dem
senkrechten
Einheitsvektor
zu
dem Oberflächenstück].
Δ×
A
oder
rot
A
ist
die
Rotation
des
Vektorfeldes
A
.
Die
rot
eines
Vektorfeldes
ist
ein
anderes
Vektorfeld,
welches
die
Rotation
des
ersten
Vektorfeldes
beschreibt;
der
Betrag
von
Δ×
A
ist
der
Betrag
der
Rotation
und
die
Richtung
von
Δ×
A
ist
die
Achse
dieser
Rotation
wie
durch
die
Rechte-Hand-Regel
beschrieben.
Wenn
man
sich
irgend
ein
3D-Vektorfeld
vorstellt,
das
eine
Strömungsgeschwindigkeit
einer
Flüssigkeit
repräsentiert,
dann
ist
die
rot
dieses
Feldes
an
einem
Punkt
angezeigt
durch
den
Weg,
den
eine
kleine
Kugel
oder
ein
Schaufelrad,
das
dort
platziert
ist,
durch
den
Fluss
gedreht
wird.
In
einem
2D-Fluss
ist
einfach
zu
sehen,
dass
die
Richtung
der
Rotationsachse
eines
Kreises
(das
2d-Gegenstück
zu
einer
Kugel)
im
Fluss
in
der
dritten
Dimension
sein
wird,
wie
sie
durch
die
Nutzung des Kreuzproduktes beim Berechnen der rot gegeben ist.
Außerdem
kann
der
Operator
Del
auf
ein
skalares
Feld
angewendet
werden.
Δ
V
oder
grad
V
ist
ein
Vektorfeld,
das
den
Gradient
der
Skalarfunktion
V
definiert.
ΔV
liegt
in
der
Richtung
des
maximalen
Anstiegs
der
Funktion
V
.
Wenn
auf
die
Potentialfunktion
angewendet,
dann
ist
grad
V
ein
Vektorfeld,
das
überall
normal
zu
den
Oberflächen
gleichen Potentials ist.
Die zwei nützlichen Eigenschaften des Operators
rot
sind:
1
.
die Divergenz des
rot
von jedem Feld ist der Nullskalar;
d.h.
, Δ
・
(Δ
×
A
) = 0
2
.
die
rot
des
Gradienten
jedes
Feldes
ist
der
Nullvektor;
d.h.
Δ×(Δf)
=
0
für
jede
Skalarfunktion
ist
abhängig
von seiner Position, wie in f(x,y,z)
Beispiel:
Zur
Visualisierung
(2)
stelle
man
sich
ein
Skalarfeld
vor
wie
ein
hügeliches
Land,
wo
die
Konturen
der
konstanten
Erhebungen
über
dem
Meeresniveau
entlang
des
Grundes
„gezogen“
werden.
Die
Erhebung
“h”
würde
dann
an
jedem
gegebenen
Punkt
(x,y,z)
mit
der
Position
variieren,
so
ist
sie
eine
Funktion
h(x,y,z).
Der
Gradient
del(h)
würde
ein
Vektor
sein,
der,
beginnend
beim
Punkt
(x,y,z),
lotrecht
zur
Konturlinie
durch
(x,y,z)
und
gerade
den
Berg
herunter
zeigt.
Man
stelle
sich
vor,
das
Wasser
fließe
den
Berg
herab
oder
welchen
Weg
eine
Murmel
rollen
würde
und
das
ist
die
Richtung
in
die
der
Gradientvektor
zeigt,
immer
lotrecht
zu
den
Konturen
mit
gleicher
Erhebung
an
jedem
Punkt.
Weil
diese
Vektoren
gerade
sind,
haben
sie
keine
rot
oder
Krümmung.
Deshalb
ist
mathematisch
’
del
×
(
del
h)
= 0′.
In
der
Praxis
bedeutet
das,
dass
ein
elektrisches
Feld,
in
welchem
die
Flusslinien
gerade
sind
(z.B.
zwischen
den
Schichten
einer
Plasmadoppelschicht
oder
einem
Kondensator,
wenn
man
die
Grenzeffekte
ignoriert,
wo
die
Linien
gerade
sind),
ein
geladenes
Teilchen
aus
seiner
Ruhe
in
gerader
Linie
beschleunigt
wird:
das
elektrische
Feld
hat keine Krümmung.
Vektorrechnung
wird
sogar
noch
wichtiger
bei
der
Analyse
der
Interaktionen
von
Teilchen,
wenn
mehrere
Kräfte
anwesend
sind,
wie
wenn
ein
geladenes
Teilchen
gleichzeitig
beide,
ein
elektrisches
Feld
und
ein
damit
verbundenes
Magnetfeld
in
einem
schrägen
Winkel
betritt,
so
dass
seine
Bewegungsvektor
eine
normale
Komponente
zu
den
Feldlinien
haben
kann
und
eine
andere
(“drift”)
parallel
zu
ihnen.
Die
Mathematica©-gestützten
Bilder
in
Kapitel
4,
§4.3,
sind
Andeutungen
der
Komplexität
von
solchen
Interaktionen
mit
nur
einem
Teilchen.
Im
Plasma
ist
die
Anzahl
von
Teilchen
um
zweistellige
Größenordnungen
größer
als
in
diesem
einfachsten
Fall
und
der
Rückkopplungsmechanismus
und
die
komplexen
Teilchenbewegungen,
die
sich
entwickeln,
veranlassen
das
Plasma
eine
Ladungstrennung
zu
schaffen
und
zu
erhalten,
Körper
mit
einem
elektrischen
Feldpotential
von
einem
Volumen
von
verschiedenem
Potential
zu
trennen,
Stromflüsse
zu
erzeugen,
Teilchen
auf
relativistische
Geschwindigkeiten
zu
beschleunigen
und
stark
zu
strahlen,
sich
einzuengen
und
Stromfolien
in
filamentäres,
leitendes
Plasma
einzurollen
wie in Blitze, koronale Schleifen und galaktische Jets.
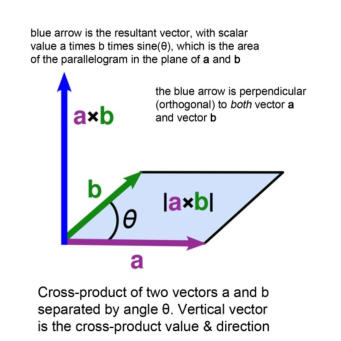
Bild von TRACE mit Arkaden von Stromschleifen und Protuberanzen über einer aktiven Region
der Sonne


- Vorwort
- Einführung
- 1. Abstände im Weltraum
- 2. Felder im Weltraum
- 3. Das Plasma
- 4. Der Elektromagnetismus
- 5. Stromfreie Doppelschichten u.a.
- 6. Ströme, Filamente und Pinche
- 7. Birkeland-Ströme und anderes
- 8. Stromschichen und -kreise
- 9. Instabilitäten
- 10. Rotationseffekte
- 11. Strahlung
- Elektrische Kometen
- Neues von Pluto
- Das Elektrische Sonnensystem
- Anhang1 - Vektoren
- Anhang2 - Maxwellsche Gleichung


- 1. Wo ist das Problem?
- 2. Wahre Wissenschaft
- 3. Wo bleibt die Mathematik?
- 4. Wo bleibt die Begutachtung?
- 5. Was ist mit der Gravitation?
- 6. Wie groß ist das Universum?
- 7. Wo ist der Leiter?
- 8. Ausbildungsdefizit?
- 9. Einstein widerlegt?
- 10. Warum Urknall bestreiten?
- 11. Was ist mit der Materie?
- 12. Elektrizität vor Magnetismus?















