
Für Anfänger
gibt es eine Einführung in die Thematik des kosmischen Plasmas unterstützt durch Youtube MoviesDer Leitfaden
der Elektro- dynamik ist die Voraussetzungen, um die Eigen- schaften des Plasmas, des Aggregatzustandes, in dem sich der Kosmos zu mehr als 99% befindet, zu verstehen..Missverständnisse
sind der Grund, warum viele Leute die Ideen des Elektrischen Universums ablehnen. Hier wird mit den Missverständnissen aufgeräumt.





Vom Mysterium der
Schöpfung zur Kernfusion
Die Vajra ist das Symbol des Thunderbolt ProjektsSpaceNews
In Kurzfilmen mit deutschen Untertiteln werden die neuesten Erkenntnisse über den Kosmos dargestellt.immer aktuell
unterstützt von
mugglebibliothek.de



Wer Interesse an der Unterstützung
dieser Website hat, melde sich
bitte bei
jasta72s@gmail.com
Willkommen bei einer
Stimme für das
Elektrische Universum
l
etzte Änderung: 11.12.2021


4. ELEKTROMAGNETISMUS
5.4.1 DIE ELEKTROMAGNETISCHEN FELDGLEICHUNGEN
Die Wissenschaft versucht physikalische Systeme mit Begriffen mathematischer Modelle zu erklären, die das Verhalten von Systemen beschreiben und vorhersagen. Kepler zum Beispiel erklärte die Bewegungen der Planeten mit seinen drei Gesetzen. In derselben Weise wird das Verhalten von Plasma durch elektromagnetische Feldgleichungen bestimmt, welche die Bewegungen der geladenen Teilchen und ihr Wechselwirken mit elektrischen und magnetischen Feldern beschreiben. Es gibt zwei Bestandteile der elektromagnetischen Feldgleichungen: Die Maxwellschen Gleichungen und die Lorentzkraft . Diese beiden Bestandteile agieren im Tandem als Rückkopplungsschleife: Die Maxwellschen Gleichungen bestimmen die elektrischen und magnetischen Felder , die auf der Position und Bewegung der geladenen Teilchen basieren. Sie bestimmen auch die Wechselwirkung elektrischer und magnetischer Felder, wenn eines davon sich ändert. Die Lorentzkraft bestimmt die elektrischen und magnetischen Kräfte zwischen geladenen Teilchen, die sich durch diese Felder bewegen. Diese Kraft veranlasst jedes Teilchen sich in Übereinstimmung mit dem Newtonschen Gesetz zu bewegen (zu beschleunigen). Die Veränderungen in den Positionen und Bewegungen der geladenen Teilchen wiederum führen zu Veränderungen in den elektrischen und magnetischen Feldern. Um diese interagierenden Phänomene in Plasmen zu verfolgen, wurden Computerprogramme entwickelt. Typischerweise beinhalten sie eine Serie von Schritten, wobei jeder nur eine kurze Zeitspanne repräsentiert. Zuerst werden unter Nutzung der Lorentzkraft und unter Berücksichtigung des Status der anwesenden magnetischen und elektrischen Felder sowie der Masse, Ladung, Geschwindigkeit und Richtung jedes Teilchens, die Kräfte berechnet, die auf jedes Teilchen des Feldes an seiner jeweiligen Position einwirken. Die Vektorsumme der beitragenden Kräfte wird berechnet und die daraus resultierende Beschleunigung der Teilchen bewegt diese eine kleine Distanz im Intervall eines winzigen Zeitschrittes (Newtons Bewegungsgesetz). Diese Berechnung wird für den ganzen Satz von Teilchen vollführt. Ausgehend von den neuen Orten und Geschwindigkeiten und Merkmalen des Satzes von Teilchen werden die Maxwellschen Gleichungen genutzt, um die Werte der elektromagnetischen Kräfte, die auf jeden neuen Ort eines Teilchens einwirken, zu bestimmen. Dann geht das Programm zurück zum ersten Schritt und berechnet die Kräfte neu, die auf den neuen Ort jedes Teilchens einwirken usw. Die Rechenschleife wird durch Programme gesteuert, die sie stoppen, wenn ein definierter Zustand erreicht ist, wie eine bestimmte Anzahl von Wiederholungen oder wenn ein bestimmter Wert der Variablen erreicht, verändert oder überschritten wurde, oder einem Fehler irgend einer Art begegnet wurde usw. Wenn eine Reihe von Startbedingungen definiert wurde (Anzahl der Teilchen, ihre Ladungen, Massen, Startgeschwindigkeiten und eine Beschreibung der Stärken der angenommenen elektrischen und magnetischen Felder in einem definierten Raumvolumen), dann kann die Bearbeitungsschleife wie folgt ausgelegt werden: 1 . Berechne alle Kräfte, die auf jedes Teilchen einwirken, mittels des Lorentzschen Gesetzes. 2 . Berechne neue Orte und Geschwindigkeiten für sehr kurze Zeitschritte unter Nutzung von Newtons Bewegungsgesetzen. 3 . Berechne E und B für neue Orte jedes geladenen Teilchens nach diesen Zeitschritten. 4 . Wenn die Endschleife noch nicht befriedigend ist, gehe zurück zu 1. und beginne die Berechnungen erneut. Ebenso können andere Aspekte für eine bessere Modellierung berücksichtigt werden, wie zum Beispiel Kollisionen von Teilchen, Reibungs- und Anziehungskräfte usw. Das ist ein komplexes Unternehmen und große Modelle mit vielen Teilchen können Monate an Rechnerzeit von Supercomputern benötigen. Diese Rückkopplungsschleife kann schnell zu hoch komplexem Verhalten führen, das mathematisch zu modellieren extrem schwierig wird. Oft werden daher Vereinfachungen vorgenommen. Doch vereinfachte Annahmen führen oft zur Vernachlässigung gerade der Verhaltensweisen von Plasma, welche es grundsätzlich von Gasen oder Flüssigkeiten unterscheiden. Leitfaden zur Blasenkammer von CERN Eine umfassende Beschreibung der elektromagnetischen Feldgleichungen ist im Anhang II zu finden. Nachfolgend aufgeführt wird eine Zusammenfassung der Hauptpunkte.4.2 DIE MAXWELLSCHEN GLEICHUNGEN
Die Aussagen der Maxwellschen Gleichungen und der ihnen zugrunde liegenden Forschungen sind die folgenden: 1 . Ein statisches elektrisches Feld kann in Abwesenheit eines magnetischen Feldes existieren, z.B. ein Kondensator oder ein Staubteilchen mit einer statischen Ladung Q hat ein elektrisches Feld ohne ein Magnetfeld. 2 . Ein konstantes Magnetfeld kann ohne ein elektrisches Feld existieren, z.B. ein Stromleiter mit einem konstanten Strom I besitzt ein magnetisches Feld ohne ein elektrisches Feld. 3 . Wo elektrische Felder zeitabhängig sind, muss ein nicht Null betragendes Magnetfeld existieren. 4 . Wo Magnetfelder zeitabhängig sind, muss ein nicht Null betragendes elektrisches Feld existieren. 5 . Magnetfelder können nur auf zwei Wegen erzeugt werden, vom Dauermagneten einmal abgesehen: durch einen elektrischen Strom oder durch ein sich änderndes elektrisches Feld. 6 . Magnetische Monopole können nicht existieren, alle Linien eines Magnetflusses sind geschlossene Schleifen.4.3 DAS GESETZ DER LORENTZKRAFT
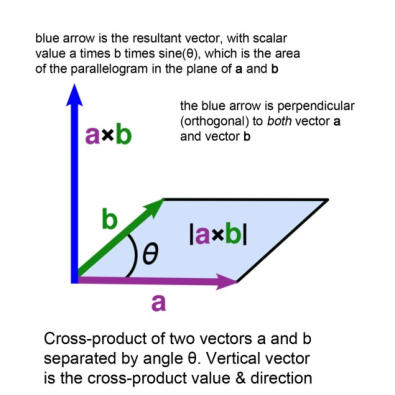
Die Lorentzkraft drückt die Gesamtkraft aus, die auf ein geladenes Teilchen einwirkt, das sowohl elektrischen als auch magnetischen Feldern ausgesetzt ist. Die resultierende Kraft bestimmt die Bewegung der geladenen Teilchen entsprechend der Newtonschen Mechanik. Da die Lorentzgleichung von grundlegender Bedeutung für das Verhalten von Plasma ist, ist sie es wert, etwas Zeit auf ihr Verstehen zu verwenden. Die Gleichung lautet: F = Q(E + U × B) (Die Vektoren sind in Fettschrift angegeben und unten erklärt) Während F die auf das Teilchen wirkende Lorentzkraft ist, ist Q die Ladung des Teilchens, E die elektrische Feldintensität, U die Geschwindigkeit des Teilchens, B ist die magnetische Flussdichte und „ x “ ist das Vektorproduktsymbol, nicht einfach ein Multiplikationszeichen. Es wird als „ U kreuz B “ gelesen. Um zu verstehen, was die Gleichung wirklich bedeutet, muss man etwas über Vektoren wissen. Ein Vektor ist eine Menge, die Größe und Richtung. Beispiele sind Richtungsgeschwindigkeit und Kraft. Ein Vektor ist wie ein Pfeil, er hat eine Länge und zeigt in eine Richtung. Im Unterschied dazu hat eine skalare Menge nur eine Größe. Beispiele sind Geschwindigkeit und Temperatur. Vektorrechnung ist die Mathematik, welche sich mit Vektoren beschäftigt. Für diejenigen, die es wissen wollen, sind weitere Details im Anhang I gegeben. Eine gute Erklärung ist auch bei Hyperphysics zu finden. Die Grundlagen für das Verständnis der Lorentzkraft werden hier erklärt. Zunächst ist die Multiplikation eines Vektors mit einer skalaren Menge wie das Aneinanderlegen einer Anzahl von Pfeilen Ende an Spitze. Der Vektor ist der erste Pfeil, die skalare Menge ist die Zahl gleicher Pfeile. Das Ergebnis ist ein größerer Pfeil, der in die gleiche Richtung zeigt wie der Originalpfeil. Ein vereinfachtes Beispiel ist die die Erhöhung der Geschwindigkeit eines Autos auf das Dreifache, wenn es sich geradlinig bewegt. Man stelle sich vor, dass der Geschwindigkeitsvektor des Autos nur ein Pfeil sei, der auf der Straße geradeaus zeigt, mit seiner Basis oder Anfangspunkt immer in der Mitte des Fahrzeugs. Man stelle sich diesen Pfeil 20 cm lang vor, um die Anfangsgeschwindigkeit von 20 km/h zu repräsentieren. Dann tritt man das Gaspedal, damit die Räder des Autos sich schneller drehen und das Auto auf eine höhere Geschwindigkeit beschleunigt wird. So wie das Auto schneller wird verlängert sich der Pfeil entsprechend der Geschwindigkeit des Autos. Bei 60 km/h ist der Pfeil 60 cm lang und seine Richtung verläuft parallel zur Straße. Wenn man das Bremspedal tritt, dann beschleunigt das Auto in die entgegengesetzte Richtung, wird langsamer und der Pfeil wird kürzer und kürzer. Wenn das Auto stoppt fällt seine Geschwindigkeit auf Null und die Länge des Geschwindigkeitsvektors wird Null. “Das ist einfach zu verstehen”, sagen Sie. “Aber was passiert, wenn ich das Steuerrad drehe, nehmen wir mal an nach links?” Diese Art von Aktion lässt eine weitere Kraft auf das Auto einwirken, in einer anderen Richtung als der, die parallel zur Mittellinie des Autos verläuft. Sie beschleunigt oder verringert die Geschwindigkeit nicht (Reibung wird vernachlässigt!), aber etwas verändert sich, weil das Auto sich dreht! Der Geschwindigkeitsvektor der Räder, der die Vorwärtsbewegung mit 60 km/h symbolisiert, hat seine Länge nicht geändert, aber eine zusätzliche Kraft wurde angewendet, so dass der Geschwindigkeitsvektor jetzt das Ergebnis zweier verschiedener Kräfte wird (zwei Pfeile, die auf das Zentrum des Autos einwirken). So lange wie man das Steuerrad im selben Winkel hält, wird dieselbe Kraft angewendet, die das Auto drehen will und es bewegt sich bei konstanter Geschwindigkeit im Kreis. So kann man sehen, dass es zwei Arten von Beschleunigung gibt: Änderungen in der Bewegungs- geschwindigkeit, entweder schneller oder langsamer – einfach nur eine Änderung im Wert des Verhältnisses von Weg pro Zeit ohne Bezug auf die Richtung – und Änderungen der Bewegungsrichtung – nur eine Winkelveränderung der Richtung im Raum von etwas sich bewegendem ohne Bezug darauf wie schnell es sich auf seinem Pfad oder seiner Bahn bewegt. Beide Arten der Veränderung sind das Ergebnis einer auf das Objekt einwirkenden Kraft. Die Multiplikation zweier Vektoren ist komplizierter. Man stelle sich eine sehr große Schraube in einem Brett vor, deren Schlitz am Kopf den ersten Vektor repräsentiert, während der zweite Vektor auf das Brett gezeichnet ist. Wenn die Schraube im Uhrzeigersinn gedreht wird, bis der Schlitz mit der Richtung des zweiten Vektors übereinstimmt, wird sich die Schraube im rechten Winkel zu beiden, dem Schlitz und dem zweiten Vektor in das Brett drehen. Der Betrag der Bewegung hängt von den Dimensionen der Schraube und dem Betrag ab, den sie gedreht wird. Das Vektorprodukt verhält sich ähnlich. Die Multiplikation zweier Vektoren unter Nutzung des Vektorproduktes resultiert in einem weiteren Vektor, der im rechten Winkel zu beiden vorhergehenden Vektoren steht. Die Richtung des neuen Vektors wird durch die Richtung der Bewegung unserer imaginären Schraube bestimmt. Die Größe (Länge) des neuen Vektors hängt von dem gedrehten Winkel und der Größe des Originalvektors ab. Im Fall unserer Schraube findet keine Bewegung der Schraube statt, wenn die Vektoren erst einmal parallel ausgerichtet sind, statt. Das Kreuzprodukt von gleich ausgerichteten Vektoren ist Null. In einem vertrauteren kartesischen Koordinatensystem wird, wenn ein Vektor in der Richtung x sich mit einem Vektor in der Richtung y kreuzt, das Ergebnis ein Vektor in der Richtung z . Die Größe des resultierenden Vektors ist das Spatprodukt der Länge der beiden Originalvektoren und des Sinuswinkels des kleineren Winkels zwischen beiden. Wenn sie parallel liegen, dann ist der Winkel zwischen ihnen Null. Da der sin(0°) Null ist, gibt es in diesem Fall keine resultierende Kraft in Richtung z . Der Effekt ähnelt sehr dem Gyroskopeffekt in kreisenden Flüssigkeiten: eine Kraft in einer Richtung führt zu einer Bewegung in einer Richtung im rechten Winkel. Das wird Periheldrehung genannt. Wenn wir zur Lorentzkraft zurückgehen, dann sehen wir, dass die Gesamtkraft sich aus zwei Teilen zusammensetzt. Der erste Teil ist QE, welcher das Produkt des Skalarwertes der Ladung eines Teilchens und eines elektrischen Feldstärkevektors ist. Die Größe der Kraft, die dem elektrischen Feld geschuldet ist, ist das Produkt der Ladung eines Teilchens und der Stärke des elektrischen Feldes. Angemerkt sei, dass, weil die dem elektrischen Feld geschuldete Kraft konstant ist und in die Richtung von E wirkt, sie eine gleichmäßige Beschleunigung auf Teilchen in der Richtung z entsprechend des Newtonschen Gravitationsgesetzes ausübt, in eine Richtung für eine positive Ladung, in die entgegengesetzte Richtung für eine negative Ladung. Der zweite Teil der Gleichung Q( U x B ) ist der interessantere. Hier haben wir zwei unter Nutzung des Kreuzproduktes mit einander multiplizierte Vektoren, die dann mit der Ladung eines Teilchens multipliziert werden. Angenommen, dass das Teilchen sich wegen seiner ursprünglichen Ausrichtung mit dem Feld nicht bewegen würde, und die Kraft Null wäre, dann wäre das Ergebnis eine Kraft, welche sich in einem rechten Winkel zu der Bewegung des Teilchens und dem Magnetfeld befindet. Diese Erklärung der Rechte Hand-Regel erklärt die lenkende Kraft, die ein Magnetfeld in einer Richtung auf geladene Teilchen ausübt, die in das Feld eintreten. Eine Kraft, die in einem rechten Winkel zur Bewegung steht, ist eine zentripetale Kraft (Definition: „Richtung des Zentrums“). Das Magnetfeld veranlasst daher die geladenen Teilchen sich in einem Kreis in einem Körper senkrecht zur Richtung des elektrischen Feldes zu bewegen. Wenn sich das Teilchen im Kreis bewegt, wird seine Geschwindigkeit an jedem Punkt immer noch eine Komponente in einem rechten Winkel zum Magnetfeld haben und es wird ebenso eine zentripetale Kraft erfahren, welche es sich weiter im Kreis bewegen lässt. Seine Richtung ändert sich ständig, doch seine skalare Geschwindigkeit ist unter diesen Bedingungen unverändert. In einem einfachen Fall ist zu berücksichtigen, was passiert, wenn ein sich bewegendes geladenes Teilchen in ein fixiertes Magnetfeld eintritt. Der Einfachheit halber ignorieren wir alle Wirkungen, die das Teilchen auf das Magnetfeld haben könnte. Wenn es in das Feld parallel zu dessen Richtung eintritt, ist es keiner Kraft ausgesetzt und seine Geschwindigkeit oder Richtung ändert sich nicht. Wenn es in das Feld in einem rechten Winkel zu der Richtung der Kraft eintritt, wird sich sein Pfad einfach nur in einen Kreis krümmen, welcher sich selbst schließt. Ohne ein elektrisches Feld lautet das Lorentzsche Gesetz (zentripetale Kraft) F = Q( U x B ). Die Kraft, die auf die geladenen Teilchen wirkt, ist direkt proportional zu Q, der Teilchenladung, zu U, dem Geschwindigkeitsvektor, und zu B, dem Magnetfeldvektor. Die Bedeutung von U x B ist U mal B mal dem Sinus des kleineren Winkels zwischen den zwei Vektoren, was bedeutet, das UB mit dem Sinuswinkel multipliziert wird, so dass seine Wirkungsreichweite zwischen 0 und 1 liegt. In der vergleichenden Illustration unten werden die Ladung des Teilchens und das magnetische Feld konstant gehalten und die Geschwindigkeit des Teilchens, das in das Feld eintritt, wächst von links nach rechts an. Je schneller das Teilchen sich bewegt, umso größer wird der Radius der resultierenden Kreisbewegung, weil der Radius r ein Maß des linearen Kraftimpulses m U des Teilchens ist, wobei m die Teilchenmasse ist: r = mU ÷ (Q|B|). Das gleiche Ergebnis würde sich ergeben, wenn die Ladung sich erhöhen würde, während die anderen beiden Variablen konstant blieben. Wenn das geladene Teilchen mit einer Bewegungskomponente in Richtung des Feldes in das Magnetfeld eintritt, z.B., in einem Winkel zwischen Null und 90 Grad zur Feldrichtung, dann „driftet“ es in eine Richtung parallel zum Feld, während die Feldkräfte das Teilchen in eine kreisförmige Bewegung zwingen. Dieser “driftende” Kreispfad führt eine Helix oder Spirale aus. Das “Lenkzentrum” des Kreises folgt einer Feldlinie des Magnetfeldes. Der Radius r ist unter dem Namen Larmor-Radius bekannt oder Zyklotronradius. In den drei Illustrationen unten bleiben der Eintrittswinkel des Teilchens und die Stärke des Magnetfeldes, B, gleich, mit einer kleinen Driftbewegung nach rechts. Die ursprüngliche Eintrittsgeschwindigkeit steigt stufenweise von links nach rechts. In der Bildserie unten zeigt der grüne Eintrittsvektor, der das Magnetfeld und die elektrischen Feldlinien berührt, auf welchem Weg ein positiv geladenes Teilchen (nach Übereinkunft) sich bewegt, wenn es in (ein) Feld(er) “eintritt”. Das Teilchen kann nach dem Eintritt in jede Richtung entlang der Vektorenlinie gehen, deshalb gehen zwei Flugbahnen von der Spitze des grünen Vektors aus, wie man sehen kann. Wenn das Teilchen negativ geladen wäre, würde es in die entgegengesetzte Richtung beschleunigt und wenn es schwerer wäre oder sich schneller bewegen würde, dann würde es einen größeren Kreisdurchmesser haben als dargestellt. In ähnlicher Weise würde bei der Änderung eines elektrischen oder magnetischen Feldes bei Konstanthaltung der anderen Faktoren das Verhaltens des Teilchens geändert. Die engen orangefarbenen Röhren repräsentieren den Pfad des Teilchens, der sich aus den Eingangsbedingungen ergibt.3. Das
Plasma
5. Plasma-Randzonen u.a.
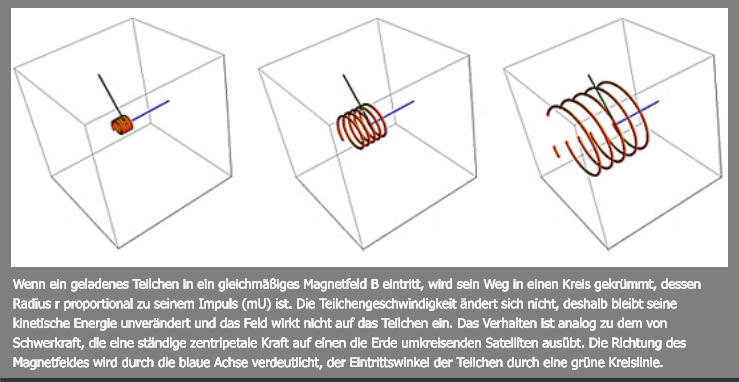
Wenn
das
geladene
Teilchen
das
vereinte,
ausgerichtete
Feld
axial
(parallel
zum
Magnetfeld)
betritt,
dann
wirkt
kein
Magnetfeld
auf
es
ein.
Daher
wird
keine
Kraft
ausgeübt,
die
es
zwingt,
sich
um
ein
Lenkzentrum
zu
drehen.
Jedoch
wird
das
elektrische
Feld
das
Teilchen
entlang
der
Feldlinien
beschleunigen.
In
Abhängigkeit
von
seiner
Ladung
wird,
wenn
das
Teilchen
in
Richtung
der
Beschleunigungskraft
eintritt,
seine
Geschwindigkeit
zunehmen.
Wenn
es
auf
Widerstand
zu
dieser
Kraft
stößt,
dann
bremst
es,
wird
vielleicht
stoppen
und
in
die
entgegengesetzte Richtung beschleunigen.
Wen
die
Felder
nicht
ausgerichtet
sind,
dann
können
verschiedene
Bahnkombinationen
vorkommen,
ganz
in
Abhängigkeit
von
der
Ladung,
Feldstärken,
Eintrittsrichtung
und
Abweichung
des
Winkels
von
der
Ausrichtung
von
magnetischen und elektrischen Feldern.

Obwohl
diese
Flugbahnen
sehr
komplex
aussehen,
beinhalten
sie
nur
ein
einziges
geladenes
Teilchen
mit
konstanten
elektrischen
und
magnetischen
Feldern
und
mit
der
gleichen
Eintrittsgeschwindigkeit.
In
der
Realität
können
viele
geladene
Teilchen
dasselbe
Volumen
im
Weltraum
auf
einmal
einnehmen
und
ihre
elektrischen
und
magnetischen Wechselwirkungen können die Werte des Feldes, in dem sie sich bewegen, beeinflussen.
Es
können
auch
neutrale
Teilchen
dabei
sein,
ebenso
wie
Staub
und
Körner
und
große
Körper,
die
alle
auch
Kräfte (Gravitation, Viskosität, Kollisionen) auf die Wechselwirkungen von Plasma zur Geltung bringen können.
Im
Vorbeigehen
halten
wir
fest,
dass
sekundäre
Effekte
von
Elektronen
mit
Geschwindigkeiten
nahe
denen
des
Lichtes,
die
sich
spiralförmig
um
Magnetfeldlinien
im
Weltraum
herum
bewegen,
oft
in
Form
von
Synchrotron
-
Strahlung
gefunden
werden.
Aus
der
Diskussion
der
Lorentzkraft
wissen
wir,
dass
es
dort
deshalb
ein
elektrisches
Feld
geben
muss,
welches
mit
einem
Magnetfeld
verbunden
ist
und
dass
die
spiralförmige,
axiale
Bewegung
der
Elektronen
mit
einer
Geschwindigkeitskomponente
parallel
zum
Magnetfeld
einen
feldabhängigen
Strom
erzeugt.
Diese Ströme sind Birkeland-Ströme, sie treten in vielen kosmischen Größenordnungen auf.
4.4 ANDERE EFFEKTE DER FELDGLEICHUNGEN
Es ist nötig sich an einige grundlegende Ergebnisse der Anwendung elektromagnetischer Feld-gleichungen zu erinnern. 1 . Elektrische Felder wirken auf alle geladenen Teilchen. 2 . Die elektrische Kraft wirkt bei gegensätzlich geladenen Teilchen in entgegengesetzte Richtungen. Deshalb erzeugt ein elektrisches Feld entgegengesetzte Richtungen von Ionen und Elektronen und tendiert so dazu, sie von einander zu trennen. Ladungstrennung im Weltraum ist in der Plasma-Physik wichtig. 3 . Magnetfelder wirken nur auf sich bewegende Teilchen. Da diese Kraft vom Kreuzprodukt von Geschwindigkeit und Feldvektoren abhängt, ist die Wirkung in verschiedene Richtungen unterschiedlich. Daraus ergibt sich ein richtungsabhängiger elektrischer Widerstand. 4 . Die Magnetkraft ist ladungsabhängig. Ionen und Elektronen kreisen deshalb in entgegengesetzten Richtungen mit unterschiedlichen Radien und Umlaufzeiten. 5 . Große Plasmamengen, die sich quer zur Richtung eines Magnetfeldes bewegen, verursachen die Entwicklung eines lokalen elektrischen Feldes, welches wiederum selbst mit neuen Kräften auf geladene Teilchen einwirkt. 6 . Veränderungen in der Verteilung der geladenen Teilchen verursachen eine Veränderung in den elektrischen Feldern zwischen ihnen, eine Veränderung des elektrischen Feldes erzeugt eine Veränderung im Magnetfeld. 7 . Die Maxwellschen Gleichungen und die Lorentzkraft wirken zusammen wie eine Rückkopplungsschleife, die die Bewegungen der geladenen Teilchen und der Felder in komplexer Weise modifizieren. 8.4.5 ERSATZ VON STRÖMEN DURCH MAGNETISCHE FELDER
Es stellt sich die Frage, ob elektrische Ströme bei der Nutzung der Maxwellschen Gleichungen durch Magnetfelder ersetzt werden können, was die Lösung viel einfacher machen würde. Die Antwort ist, technisch gesehen, ja, das können sie in bestimmten einfachen Situationen. Das wird auch oft in magneto-hydrodynamischen Theorien und Modellen getan, weil es beim Studium bestimmter Plasmaverhaltensweisen bequemer ist. Es gibt jedoch viele Aspekte des Plasmaverhaltens, wo es notwendig und entscheidend ist, die Bewegungen geladener Teilchen zu berücksichtigen, weil die einfache Berücksichtigung des Feldverhaltens das beobachtete komplexe Verhalten von Plasma nicht modellieren kann. Diese Situation verhält sich analog zu der Welle-Teilchen-Dualität in der Teilchenphysik: es gibt einige Situationen, wo es nötig ist, die teilchen- bezogene Beschreibung zu verwenden. Beispiele des Plasmaverhaltens, die die Nutzung der Teilchen- oder Strombeschreibung erfordern, schließen die Zellbildung und Filamentierung, den Energietransport und Instabilitäten ein. Die Berücksichtigung von elektrischen Strömen und Kreisläufen verlangt ebenfalls die Nutzung der auf Teilchen beruhenden Beschreibung. Die bloße Berücksichtigung der Feldeffekte in diesen Situationen wird der wahren Komplexität des Verhaltens von Plasma nicht gerecht. Wir werden jetzt auf einige dieser komplexen Verhaltensweisen näher eingehen.






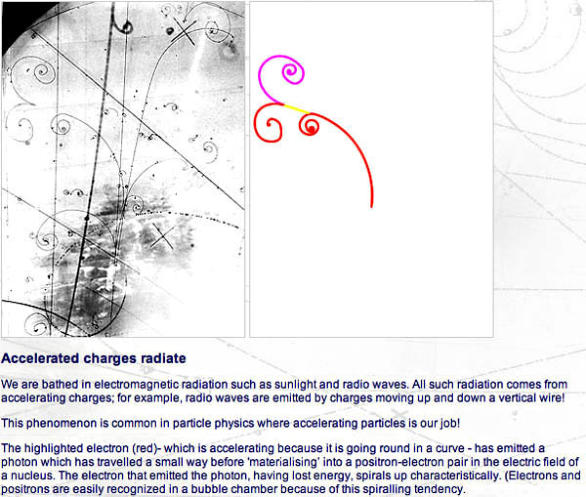
Eine Blasenkammer innerhalb eines Magnetfeldes erzeugt sichtbare Spuren geladener Teilchen, die
die Beurteilung von Teilchen-Energien, Wechselwirkungen und Kollisions-nebenprodukten erlauben,
wenn sie zusammen mit einem Teilchenbeschleuniger installiert wird. Bildquelle. Der Leitfaden zur
Blasenkammer wurde von CERN bereit gestellt (Link siehe unten)
Die
Gesamtkraft
ist
das
Ergebnis
der
Vektoren
der
elektrischen
und
magnetischen
Kräfte
und
abhängig
vom
Winkel zwischen den beiden Feldern (Bilder unten).
Wenn
elektrisches
und
magnetisches
Feld
parallel
verlaufen
(wie
in
dem
am
Feld
ausgerichteten
Strom,
den
wir
später
betrachten),
dann
wird
ein
geladenes
Teilchen,
das
sich
kreisförmig
entlang
der
Achse
der
Felder
annähert,
gezwungen
sich
in
einer
spiralförmigen
Bahn
zu
bewegen,
die
an
der
Richtung
der
Felder
ausgerichtet
ist.
Das
bedeutet,
dass
Teilchen
bewegt
sich
spiralförmig
um
die
Achsenrichtung
des
Magnetfeldes
aufgrund
der
Wirkung
der
Lorentzkraft
und
beschleunigt
in
die
Richtung
des
elektrischen
Feldes.
Das
lässt
die
nachfolgenden
Drehungen
weiter
und
weiter
auseinander
erfolgen,
wenn
die
Teilchengeschwindigkeit
in
der
E-Feldrichtung
mit
der
Zeit steigt.
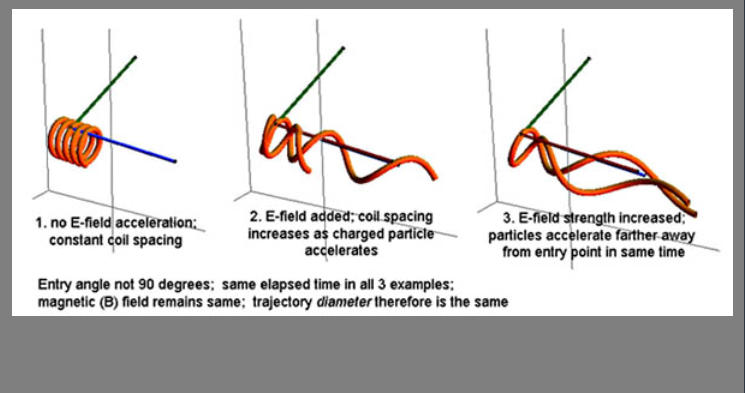
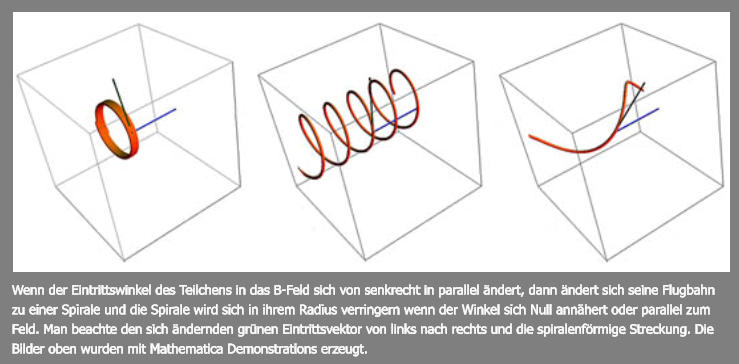
In dieser am Feld ausgerichteten Situation ( E- und B-Feld parallel) wird ein Teilchen auf einer Bahn, die zur selben Zeit der
Einwirkung der zentripetal kreisenden Magnetkraft sowie dem E-Feld-Vektor (rot) unterliegt, gezwungen axial zu
beschleunigen. Nach einer Weile bewegt sich das Teilchen fast parallel zu den Feldern.
Beim Vorhandensein eines konstanten elektrischen Feldes gibt es eine generelle Tendenz, die beschleunigten Teilchen
immer enger an seinen Feldlinien auszurichten und die Geschwindigkeit zu steigern. Die Bilder oben wurden mit
Mathematica Demonstrations erzeugt.
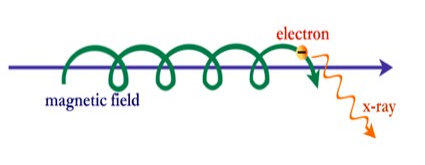
Ein am Feld ausgerichtetes, schnelles Elektron erzeugt
Synchrotronstrahlung im Röntgenwellenbereich.

Die Galaxie Centaurus besitzt, wie man auf dieser Röntgenlichtaufnahme
von Chandra sehen kann, einen zentralen Plasmajet und daraus
resultierende Wolkenstrukturen, die sich über Zehntausende Lichtjahre
erstrecken
Übersetzung H.Täger
3. Das Plasma
Plasma-Randzonen u.a.


- Vorwort
- Einführung
- 1. Abstände im Weltraum
- 2. Felder im Weltraum
- 3. Das Plasma
- 4. Der Elektromagnetismus
- 5. Stromfreie Doppelschichten u.a.
- 6. Ströme, Filamente und Pinche
- 7. Birkeland-Ströme und anderes
- 8. Stromschichen und -kreise
- 9. Instabilitäten
- 10. Rotationseffekte
- 11. Strahlung
- Elektrische Kometen
- Neues von Pluto
- Das Elektrische Sonnensystem
- Anhang1 - Vektoren
- Anhang2 - Maxwellsche Gleichung


- 1. Wo ist das Problem?
- 2. Wahre Wissenschaft
- 3. Wo bleibt die Mathematik?
- 4. Wo bleibt die Begutachtung?
- 5. Was ist mit der Gravitation?
- 6. Wie groß ist das Universum?
- 7. Wo ist der Leiter?
- 8. Ausbildungsdefizit?
- 9. Einstein widerlegt?
- 10. Warum Urknall bestreiten?
- 11. Was ist mit der Materie?
- 12. Elektrizität vor Magnetismus?















