
Für Anfänger
gibt es eine Einführung in die Thematik des kosmischen Plasmas unterstützt durch Youtube MoviesDer Leitfaden
der Elektro- dynamik ist die Voraussetzungen, um die Eigen- schaften des Plasmas, des Aggregatzustandes, in dem sich der Kosmos zu mehr als 99% befindet, zu verstehen..Missverständnisse
sind der Grund, warum viele Leute die Ideen des Elektrischen Universums ablehnen. Hier wird mit den Missverständnissen aufgeräumt.





Vom Mysterium der
Schöpfung zur Kernfusion
Die Vajra ist das Symbol des Thunderbolt ProjektsSpaceNews
In Kurzfilmen mit deutschen Untertiteln werden die neuesten Erkenntnisse über den Kosmos dargestellt.immer aktuell
unterstützt von
mugglebibliothek.de



Wer Interesse an der Unterstützung
dieser Website hat, melde sich
bitte bei
jasta72s@gmail.com
Willkommen bei einer
Stimme für das
Elektrische Universum
l
etzte Änderung: 11.12.2021
8. PLASMA-STROMSCHICHTEN, VERTIKALE
STRÖME UND ELEKTRISCHE STROMKREISE
8.1 PLASMA-STROMSCHICHTEN
Es wurde bereits auf die Filamentierung von Stromschichten hingewiesen. Dieser Abschnitt wird das Wesen der Stromschichten und ihre Beziehung zum Magnetfeld erkunden.
Eine
Stromschicht
ist
genau,
was
der
Name
sagt
–
eine
dünne
Oberfläche,
in
der
ein
Strom
fließt.
Sie
unterscheidet
sich
ganz
offensichtlich
von
einer
sich
bewegenden
Ladung
und
von
zylindrischen
Stromfilamenten.
Eine
Stromschicht
bildet
eine
Oberfläche
zwischen
zwei
Regionen
von
Plasma,
etwa
wie
eine
Doppelschicht
(DL),
und wie DL teilt sie sich oft in Regionen mit unterschiedlichen Eigenschaften auf.
Der
Strom
fließt
in
den
Schichten
in
eine
Richtung,
die
vollständig
innerhalb
der
Schicht
enthalten
ist.
Man
kann
sich
das
so
vorstellen,
als
würde
der
Strom
auf
gekrümmten
Pfaden
durch
ein
gewebtes
Leinenbettuch
fließen:
alle
Ströme
fließen
in
den
gekrümmten
Pfaden
in
dieselbe
Richtung
und
keine
Strom
fließt
in
den
Schussfäden.
Ein
Strom
besteht
natürlich
aus
Ionen
und
Elektronen,
die
in
entgegengesetzte
Richtungen
fließen,
deshalb
enthält
die
Stromschicht beide Teilchenarten.
Die
Richtung
des
Stroms
kann
sich
offensichtlich
ändern,
da
die
Schicht
selber
nicht
eben
sein
muss.
So
gibt
es
zum
Beispiel
klare
Beweise
für
teilweise
gerundete
Stromschichten
am
“bow
shock”
[Bogenschock],
wo
die
Magnetosphäre der Erde mit dem ankommenden Sonnenwind interagiert.
Wenn
wir
das
Magnetfeld
nahe
der
Stromschicht
analysieren,
dann
finden
wir,
dass
die
Magnetkraft
wegen
der
Stromschicht
auf
jeder
Seite
in
der
entgegengesetzten
Richtung
wirkt.
Wenn
zum
Beispiel
ein
Strom
diese
Seite
hoch
fließt,
dann
wird
das
Magnetfeld
über
der
Seite
von
links
nach
rechts
gehen
und
unter
der
Seite
wird
es
von
rechts
nach
links
verlaufen,
wie
man
es
erwartet
von
der
Rotation
der
Rechte-Hand-Regel
für
jeden
einzelnen
“Faden”
des
Stroms.
(Man
beachte,
dass
die
Rotations-Rechte-Hand-Regel
nicht
dasselbe
ist
wie
die
Rechte-Hand-Regel
des
Vektorkreuzproduktes!)
Deshalb
ist
es
ein
genereller
Effekt
von
Stromschichten
separate
Gebiete
von
entgegengesetzten
Magnetfeldern
zu
erzeugen
.
Am
Ort
der
Schicht
selber
ist
das
Magnetfeld
Null.
Das
ist
exakt
die
Situation,
die
im
Schweifgebiet
des
Magnetfeldes
der
Erde
gefunden
wurde,
wo
eine
Stromschicht
in
der
Äquatorialebene
zwei
Zonen
entgegengesetzter
Magnetfelder
von
einander
trennt.
In
diesem
Fall
fließt
der
Strom
der
Schweifschicht
azimutal
oder
von
“West
nach
Ost”
und
die
Magnetfelder
liegen
radial,
ausgerichtet
zur
Erde
in
der
nördlichen
Hemisphäre
und
von
der
Erde
weg
in
der südlichen Hemisphäre.
Das
Gravitationsmodell
beschreibt
diese
Stromschichten
als
verursacht
durch
die
an
einer
Seite
entgegengesetzten
Magnetfelder.
Erinnern
wir
uns
daran,
dass
magnetische
Felder
Kraftfelder
sind,
die
durch
die
Bewegung
geladener
Teilchen
verursacht
werden,
dass
heißt,
durch
Ströme,
so
dass
das
Gravitationsmodell
Ursache
und
Wirkung
zu
verwechseln
scheint.
Was
die
magnetischen
Felder,
die
der
Strom
erzeugt,
tatsächlich
tun,
das
ist
das
Zusammenpressen des Stromes in Form der Schicht. Sie erzeugen aber keinen Strom.
Stromschichten
sind
deshalb
ein
anderes
Mittel
durch
das
Plasma
als
Reaktion
auf
eine
sich
verändernde
Umgebung Zellen bildet.
Stromschichten
können
auch
bewirken,
dass
Massen
in
einer
Anwendung
gepulster
Plasmadüsen
beschleunigen. Siehe Text und Video vom Princeton University Electric Propulsion and Plasma Physic Lab
hier
.
8.2 VERTIKALE STRÖME
Wir haben bereits die Fälle berücksichtigt, wo Ströme parallel (am “Feld ausgerichtet” sind) zum Magnetfeld (Filamente und Birkeland-Ströme) fließen und den Fall, wo Ströme in Regionen eines Nullfeldes (Stromschichten) fließen. Die übrig gebliebene Möglichkeit für Ströme ist, eine Vektorkomponente zu haben, die vertikal zum Magnetfeld unter dem Einfluss nichtmagnetischer Kräfte in Verbindung mit dem Magnetfeld wirkt (siehe 8.3 unten). [Erinnert sei daran, dass F die resultierende Vektorkraft eines geladenen Teilchens ist; q ist der Wert für den Betrag der Ladung eines Teilchens; E ist der Vektor des elektrischen Feldes zu einer bestimmten Zeit an einem bestimmten Koordinatenpunkt; U ist der Geschwindigkeitsvektor eines geladenen Teilchens zu einer bestimmten Zeit an einem bestimmten Koordinatenpunkt, und B ist der magnetische Feldvektor zu einer bestimmten Zeit an einem bestimmten Koordinatenpunkt. Schließlich sei noch angemerkt, dass die Vektoren in Fettschrift sich auf eine skalare Größe beziehen und eine Richtung, z.B. 3000 km/s Richtung Osten.] Die Lorentzkraft auf geladene Teilchen, F = q( E + U x B ) in der Vektorrechnung, hängt ab von der Beziehung der Geschwindigkeit des Teilchens U zum Magnetfeld B . Die Größe des Vektorkreuzproduktes U x B kann geschrieben werden als UB sin θ, wobei θ der kleinere Winkel zwischen U und B ist. Die Richtung der Kraft, die von U x B erzeugt wird, wird durch die Bewegung der rechtshändigen Schraube angegeben, die sich von U nach B dreht, d.h. im rechten Winkel zu beiden, U und B . Das führt dazu, dass sich geladene Teilchen im rechten Winkel zum Magnetfeld bewegen, um einem kreisförmigen Pfad in einer zum Feld senkrechten Ebene zu folgen. Wir können das die zentripedale Kraft nennen. Wenn E ungleich Null ist, wird das Teilchen auch in die Richtung von E beschleunigt. Wenn U Null ist oder parallel zu B, dann gibt es offensichtlich keine zentripedale Kraft, die vom Magnetfeld auf das Teilchen wirkt. Mit anderen Worten, wenn das Teilchen stationär ist oder sich parallel zum Feld bewegt, dann wird es keine magnetische Kraft erfahren. Anstatt veränderliche Winkel zwischen U und B zu berücksichtigen, ist es einfacher die parallelen und vertikalen Komponenten von U separat zu berücksichtigen. Da nur die vertikalen Komponente eine Kraft verursacht, können wir uns auf diese Komponente allein konzentrieren. Wir werden auch annehmen, dass E = 0 ist, solange es nicht anders gesagt wird. Die Teilchengeschwindigkeit, die sich aus der Kombination einer kraftbedingten Bewegung und eines Magnetfeldes ergibt, kann als Kreisbewegung um ein lenkendes Zentrum angenommen werden (Bild unten), wobei das Zentrum selbst wiederum vertikal zum Magnetfeld mit der Geschwindigkeit v p driftet, entsprechend der Lenkzentrumsgleichung: v p = (F × B) / qB² Man beachte, dass F eine nichtmagnetische Kraft ist (z.B. Gravitation oder ein elektrisches Feld), welche die Bewegung der geladenen Teilchen verursacht. Diese Bewegung wechselwirkt dann mit dem Magnetfeld entsprechend des Lorentzschen Gesetzes. Wenn B in die Richtung z geht und F in die Richtung y im Kartesianischen Koordinatensystem, dann geht die resultierende Geschwindigkeit in die Richtung x .
Was
uns
diese
Gleichung
sagt,
ist,
folgendes:
Wenn
ein
Teilchen
Gegenstand
einer
externen
Kraftwirkung
vertikal
zum
Magnetfeld
ist,
dann
wird
es
eine
konstante
Geschwindigkeit
vertikal
zu
beiden,
dem
Feld
und
der
Kraft,
annehmen. Wie das geschieht, wird nachfolgend dargestellt:
Wenn
ein
Teilchen
ursprünglich
ruht,
wird
eine
externe
Kraft
(sagen
wir
ein
elektrisches
Feld)
beginnen
es
in
die
Richtung
der
Kraft
entsprechend
des
Newtonschen
Gesetzes
zu
beschleunigen.
Sobald
jedoch
das
Teilchen
einen
kleinen
Betrag
an
Geschwindigkeit
oder
eine
Geschwindigkeitskomponente
vertikal
zum
Magnetfeld
erworben
hat,
dann
taucht
im
Ergebnis
des
Magnetfeldes
eine
zentripedale
Kraft
auf
und
beginnt
den
Pfad
des
Teilchens
von
der
Flugbahn, die durch die externe Kraft erzeugt wird, wegzudrehen.
Die
externe
Kraft
versucht
immer
noch
das
Teilchen
in
Richtung
der
Kraft
zu
beschleunigen,
doch
dort
gibt
es
jetzt
eine
Komponente
der
zentripedalen
Kraft,
welche
der
externen
Kraft
entgegenwirkt.
Die
Beschleunigung
in
Richtung der externen Kraft wird dementsprechend reduziert.
Unter
dem
Einfluss
beider,
der
externen
und
der
zentripedalen
Kraft,
wird
das
Teilchen
einem
gekrümmten,
sich
um
90
Grad
drehenden
Pfad
folgen.
An
dem
Punkt,
wo
der
Pfad
senkrecht
zur
externen
Kraft
verläuft,
hat
das
Teilchen
die
Geschwindigkeit
v
p
entsprechend
der
Gleichung
des
lenkenden
Zentrums
erworben,
und
die
zentripedale
Kraft
gleicht die externe Kraft wegen der Wechselwirkung von
v
p
und
B
genau aus.
Deshalb
gibt
es
weder
eine
weitere
Beschleunigung
in
Richtung
der
externen
Kraft
noch
irgendeine
Beschleunigung
in
Richtung
von
v
p
,
weil
es
keine
Kraft
in
dieser
Richtung
gibt.
Das
Teilchen
hat
eine
konstante
Geschwindigkeit erhalten, lotrecht zu beiden, zu
B
und der externen Kraft.
So
lange
wie
das
Teilchen
seine
Bewegung
mit
der
Geschwindigkeit
v
p
in
der
lotrechten
Richtung
fortsetzt,
so
lange ist die Situation stabil und die externe Kraft bleibt durch die zentripedale Kraft im Gleichgewicht.
8.3 EFFEKTE VERSCHIEDENER EXTERNER KRÄFTE
Die obigen Überlegungen beziehen sich auf jede konstante externe Kraft, die auf geladene Teilchen in einem Magnetfeld einwirkt. Verschiedene Kräfte können Beschleunigungen in vertikaler Richtung zum Magnetfeld verursachen. Diese schließen Gravitation, ein elektrisches Feld und Drehmomente ein . Jede wird einen anderen Effekt in Abhängigkeit davon haben, ob die externe Kraft eine Funktion der Masse oder der Ladung des Teilchens ist und zwar wie folgt: Fall A. Elektrische Feldkraft, F E × B für ein elektrisches Feld vertikal zu B . Weil F E = q E ist, wird die Lenkzentrumsgleichung: v p = ( E × B ) / B 2 In Fall A ist die vertikale Geschwindigkeit unabhängig von der Ladung des Teilchens. Daraus ergibt sich ein spezieller Fall von Ionen und Elektronen, die in die gleiche Richtung driften, wie wir bei der Betrachtung der Konzentration von Materie durch filamentäre Ströme sahen. Fall B. Gravitation, F g × B Weil F g = m g ist, hängt die resultierende vertikale Driftgeschwindigkeit von der Masse der Teilchen und ihrer Ladung ab, und für Fall B gilt: v p = (g × B) × m/qB² • Ionen und Elektronen bewegen sich deshalb in entgegen gesetzte Richtungen, woraus sich in einem Strom Ladungstrennung ergibt und Zonen verschiedenen Potentials (z.B. elektrische Felder). All diese Effekte kommen einfach als Resultat der Wechselwirkung zwischen Gravitation und Magnetfeld vor. Offenbar beginnen diese Effekte dann ihre eigenen sekundären Wirkungen/Effekte zu verursachen und daraus kann sich komplexes Plasmaverhalten ergeben. (Ref: Fundamentals of Cosmic Electrodynamics, Boris V. Somov, Kluwer Academic Publishers, 1994, Chapter 2,Motion of a Charged Particle in Given Fields ) • Zusätzlich kann die Abhängigkeit der Geschwindigkeit von der Masse der Teilchen auch in einer chemischen Trennung verschiedener Ionen oder Marklund-Konvektion resultieren. • Ein Fall ist hier von besonderem Interesse. Wenn man die Erde und ihr Magnetfeld betrachtet, kann es verbildlicht werden als Feldlinien, die sich in den nahen Weltraum ausdehnen, die etwa so angeordnet sind wie die Segmente einer Orange. In der äquatorialen Ebene ist das Feld Nord-Süd ausgerichtet. Die Gravitationskraft wirkt radial einwärts und so in einem rechten Winkel zum Feld. • Irgendwelche Ionen oder Elektronen in der Umgebung, zum Beispiel in der Atmosphäre, erlangen daher Geschwindigkeiten vertikal zu beiden, B und g, unter dem kombinierten Einfluss von Gravitation und Magnetfeld. Weil die Beschleunigung von Ionen und Elektronen in entgegengesetzte Richtungen erfolgen, ist dies das Äquivalent zu einem Strom, der in einem Ring um die Äquatorialebene fließt. Die Van Allen-Gürtel sind Beispiele für Ringströme. • Das ist ein unvermeidliches Resultat der Anwesenheit geladener Teilchen in einem Magnetfeld, das im rechten Winkel zum Gravitationsfeld ausgerichtet ist. In dieser Situation wird immer ein Strom erzeugt. Mehrere der Monde des Jupiters und des Saturns zeigen diese Ströme, die durch elektromagnetische Strahlung nachgewiesen sind, dort, wo die erzeugten Ströme mit den Atmosphären der Planeten in der Umgebung ihres polaren Auroraovals in Kontakt kommen.







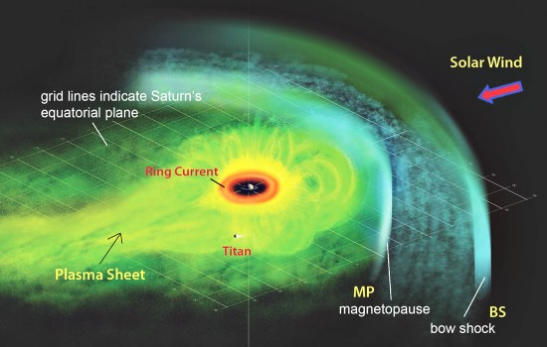
Vorstellung eines Künstlers von der Plasmaschicht des Saturns, basierend auf Cassinis magne-
tosphärischem Bildinstrument. Die Plasmaschicht trennt die Hälften der oberen und unteren
Magnetosphäre, dünnt sie in Richtung der Nachtseite des Planeten allmählich aus. Die Mag-
netopause deutet den Fluss des abgelenkten Solarwindes an.
Bildquelle: NASA/Jet Propulsion Laboratory / Johns Hopkins University Applied Physics
Laboratory.
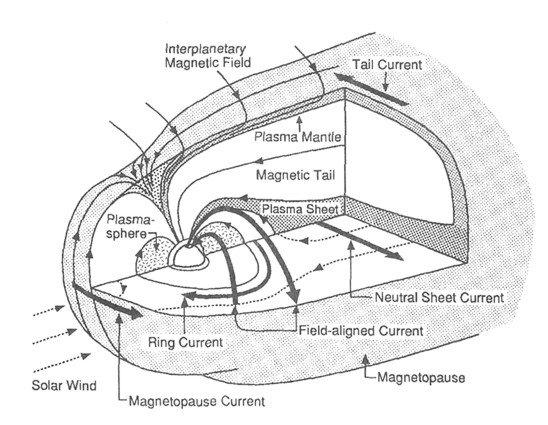
Schnittbild der Plasma-Stromschichten der Erde in- und außerhalb der Magnetosphäre.
Bildquelle: Wikipedia images, zahlreiche Webseiten ohne Quellennachweis
Schnittbild der Plasma-Stromschicht der Erde in und um ihre Magnetosphäre.
Bildquelle: Wikipedia Images, zahlreiche andere Webseiten ohne Quellenangabe
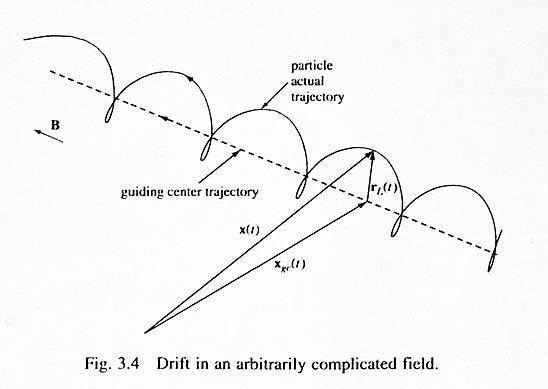
Spiralförmige Bahn eines geladenen Teilchens, mit seiner Kreisbewegung überlagert von
seinem Driftgeschwindigkeitsvektor.
Bildquelle: „Fundamentals of Plasma Physics“, Cambridge Press, 2006; Dr. Paul Bellan,
Calofornia Institute of Technology
Fall C
. Drehmoment
F
i
= -m (d
u
/
dt)
(Newtons Zweites Bewegungsgesetz)
In
diesem
Fall
haben
die
geladenen
Teilchen
bereits
ein
ursprüngliches
Drehmoment
mu
(Inertialmasse
mal
Geschwindigkeitsvektor),
wenn
sie
einem
Magnetfeld
begegnen.
Die
Lenkzentrumsgleichung
deutet
an,
dass
das ursprüngliche Drehmoment durch das Magnetfeld verändert wird:
v
p
= -mq/B² du/dt × B
Da
v
p
ladungsabhängig
ist,
erfolgt
die
Beschleunigung
von
Ionen
and
Elektronen
in
entgegengesetzte
Richtungen
und
repräsentiert
daher
einen
Strom.
Ionen
mit
unterschiedlichen
Massen
werden
unterschiedliche
Endgeschwindigkeiten erreichen und sich so chemisch sortieren. Das ist ein anderer wichtiger Effekt der Trägheit:
Wenn
eine
Menge
an
Plasma
auf
eine
bestimmte
Geschwindigkeit
beschleunigt
wird,
zum
Beispiel
durch
eine
Kraft
I
×
B
in
der
Region
(welche
sich
entgegengesetzt
bewegende
Ionen
und
Elektronen
in
dieselbe
lotrechte
Richtung
beschleunigt),
dann
hat
das
Plasma
zu
Lasten
des
Stromkreises,
der
den
Strom
antreibt,
eine
kinetische
Energie erworben.
Wenn
diese
Menge
sich
bewegenden
Plasmas
dann
in
eine
andere
Region
eintritt,
wo
es
einen
Stromkreis
in
einem
lokalen
Plasma
erzeugen
kann,
dann
wird
seine
Geschwindigkeit
v
p
einen
Strom
vertikal
zu
beiden,
B
und
v
p
,
erzeugen.
Die
Wechselwirkung
dieses
Stroms
mit
B
wird
eine
Kraft
im
sich
bewegenden
Plasma
verursachen,
die
es
verlangsamt.
Mit
anderen
Worten,
die
kinetische
Energie
des
Plasmas
wird
wieder
aufgegeben
dadurch,
dass
ein
Strom an einem neuen Ort erzeugt wird.
Deshalb
ist
die
Wechselwirkung
der
ursprünglichen
Bewegung
geladener
Teilchen
und
ihrer
Magnetfelder
ein
Mittel
durch
welches
kinetische
Energie
mit
elektromagnetischer
Energie
ausgetauscht
werden
kann
und
deshalb
ist
es
ein Mittel durch welches Energie zwischen verschiedenen Orten transportiert werden kann
.
8.4 ELEKTRISCHE STROMKREISE IM PLASMA
Solange eine Ladung nicht von einer elektrostatischen Quelle fließt oder zu einer Senke, solange ist sie Teil eines geschlossenen Stromkreislaufes. Im Weltraum ist der Stromkreislauf nicht immer offensichtlich, weil die Leiter oft unsichtbar sind und sie den Stromkreis in sehr großer Entfernung vom interessierenden Gebiet schließen können, aber sie müssen ihn irgendwo schließen. Die Berücksichtigung der Stromkreise im Weltraum kann Verhaltensweisen erklären wie den Transport von Energie von einem Gebiet zu einem anderen, welcher spürbare elektrische Aktivitäten in der untersuchten Region antreibt. In diesem Zusammenhang ist es notwendig darauf zu verweisen, dass, wenn sich ein Plasma, welches irgendwelche Bereiche eines leichten Ladungsungleichgewichtes beinhaltet und sich relativ zu einer anderen Plasmaregion in einem Magnetfeld bewegt, es dann in der erstgenannten Region ein elektrisches Feld erzeugen wird sowie Ströme in der zweiten Region. Das geschieht wegen der Wechselwirkung der elektromagnetischen Felder und Kräfte. Das Gravitationsmodell besagt, dass das Debye screening, welches wegen ähnlicher Effekte die Ursache für eine Debye-Randschicht um einen geladenen Körper sei, das Ausmaß der Ladungsungleichgewichte zugunsten der Debye-Länge begrenzen würde. Es ist jedoch die Kraft v × B aus der Lorentzgleichung unabhängig von der Debye- Länge und sie kann ein elektrisches Feld in einer anderen Region des Plasmas weit jenseits der Debye-Grenze erzeugen.8.5 DOPPELSCHICHTEN ALS ELEMENTE DES STROMKREISES
Jede Doppelschicht beschleunigt Ionen und Elektronen wegen des Potentialgefälles der DL. Wenn die DL ein Strom führende DL ist, dann formt sie sich praktisch als Teil eines elektrischen Stromkreises, in welchem der Strom fließt. Die Energie zur Beschleunigung der Teilchen wird durch den Stromkreis bereit gestellt und innerhalb der DL in kinetische Energie umgewandelt. Die DL agiert deshalb als ein (Eingangs-)Widerstand und kann eine Reaktion erfahren, welche ihre Position driften lässt. Das erfolgt analog zu dem Rückstoß eines Gewehrs, wenn seine Kraftquelle die Masse des Geschosses beschleunigt. Die durch die DL beschleunigten Teilchen verursachen einen Druck auf das sie umgebende Plasma mit dem sie wechselwirken und erzeugen Strahlung. Der Verlust überschüssiger Energie auf diesem Wege kann es dem Plasma erlauben durch die Formung einer DL, die den notwendigen Mechanismus bereitstellt, einen stabilen Zustand zu erreichen.8.6 ENERGIE UND INDUKTIONSWIDERSTAND
Die vom Stromkreis der DL bereitgestellte Energie kann von der Energie stammen, die im Magnetfeld oder in der kinetischen Energie des Hauptteils des Plasmas gespeichert ist. In der Terminologie der Stromkreise ist ein Element, welches Energie speichert, eine Spule. Das Plasma kann man sich deshalb analog zu einer Spule in einem einfachen Stromkreis vorstellen. Ähnlich verhält sich die DL in einiger Hinsicht wie ein Kondensator, allerdings einer mit variablen Merkmalen, einschließlich eines Widerstandes, der sich mit steigendem Strom verringern kann. Alle elektrischen Stromkreisläufe, welche einen Widerstand haben, sind potentiell instabil, in Abhängigkeit von der Stromstärke, dem induktiven Widerstand, dem Widerstand und der Kapazität im Stromkreis. Wenn der Gesamtwiderstand des Stromkreises negativ ist, was im Plasma wegen der fallenden Charakteristik der I-V-Kurve (Stromspannung gegen –stärke) oft der Fall ist , dann wird die Stabilität des Induktionskreises unmöglich gemacht. Ein einfacher Stromkreis, der Stromstärke, Induktanz und negativen Widerstand einschließt, wird entweder schwingen oder all seine Energie abbauen und verschwinden. Wenn das Potenzialgefälle entlang der DL größer ist als das Plasmapotential, dann wird die DL als starke DL klassifiziert. Eine starke DL reflektiert Teilchen, die sich der DL mit weniger Energie als das Plasmapotential annähern. Nur solche Teilchen, deren Energien über dem Plasmapotential liegen, werden in die DL eintreten und durch ihr Stromstärkedifferential , d.h. ihr elektrisches Feld, beschleunigt. Das Verhalten von Plasma in einer CCDL ist deshalb anhängig von den Merkmalen des externen Stromkreises, welcher die Entstehung einer CCDL antreibt.8.7 RESONANTE STROMKREISE
Ein Stromkreis, der eine Spule und einen Kondensator enthält, hat eine natürliche oder resonante (mitschwingende) Frequenz bei der er elektrische schwingt. in ähnlicher Weise wird ein Plasmastrom, der einen Induktor in der Gestalt gespeicherter magnetischer Energie und eine CCDL mit negativem Widerstand besitzt, dazu tendieren, eine resonante Schwingung zu haben, bei der Energie zwischen dem elektrischen Feld in der DL und dem Magnetfeld im Plasma ausgetauscht wird. Wenn das elektrische Feld in der DL sich erhöht, dann beschleunigt es in der normalen Weise Teilchen auf höhere Energieniveaus. Es ist offensichtlich, dass dieses Modell ein wirksames Mittel zur Erzeugung hochfrequenter Strahlungausstöße ist. Im Gegensatz dazu postuliert das Gravitationsmodell, dass sehr hoch verdichtete Neutronensterne bis zu Tausende male pro Sekunde rotieren würden, um dieses häufig beobachtete Phänomen zu erklären. Nicht alle Situation führen zu einer resonanten Frequenz. Variationen führen oft zum Auftreten von Schwingungen über ein weites Frequenzband. In Begriffen des elektrischen Stromkreises ist die DL dann “geräuschvoll”. Die Wirkung des Geräusches besteht darin eine Bandbreite von Elektronenenergien in dem Strahl zu erzeugen, der durch die DL beschleunigt wird. Einige Elektronen haben dann genug Energie, um aus dem Magnetfeld auszubrechen, das den Strom einschnürt und das kann zur Expansion des Plasmas führen. Übersetzung H. Täger9. Plasmainstabilitäten
7. Birkelandströme und anderes
9. Plasmainstabilitäten
7. Birkelandströme und anderes


- Vorwort
- Einführung
- 1. Abstände im Weltraum
- 2. Felder im Weltraum
- 3. Das Plasma
- 4. Der Elektromagnetismus
- 5. Stromfreie Doppelschichten u.a.
- 6. Ströme, Filamente und Pinche
- 7. Birkeland-Ströme und anderes
- 8. Stromschichen und -kreise
- 9. Instabilitäten
- 10. Rotationseffekte
- 11. Strahlung
- Elektrische Kometen
- Neues von Pluto
- Das Elektrische Sonnensystem
- Anhang1 - Vektoren
- Anhang2 - Maxwellsche Gleichung


- 1. Wo ist das Problem?
- 2. Wahre Wissenschaft
- 3. Wo bleibt die Mathematik?
- 4. Wo bleibt die Begutachtung?
- 5. Was ist mit der Gravitation?
- 6. Wie groß ist das Universum?
- 7. Wo ist der Leiter?
- 8. Ausbildungsdefizit?
- 9. Einstein widerlegt?
- 10. Warum Urknall bestreiten?
- 11. Was ist mit der Materie?
- 12. Elektrizität vor Magnetismus?















