
Für Anfänger
gibt es eine Einführung in die Thematik des kosmischen Plasmas unterstützt durch Youtube MoviesDer Leitfaden
der Elektro- dynamik ist die Voraussetzungen, um die Eigen- schaften des Plasmas, des Aggregatzustandes, in dem sich der Kosmos zu mehr als 99% befindet, zu verstehen..Missverständnisse
sind der Grund, warum viele Leute die Ideen des Elektrischen Universums ablehnen. Hier wird mit den Missverständnissen aufgeräumt.





Vom Mysterium der
Schöpfung zur Kernfusion
Die Vajra ist das Symbol des Thunderbolt ProjektsSpaceNews
In Kurzfilmen mit deutschen Untertiteln werden die neuesten Erkenntnisse über den Kosmos dargestellt.immer aktuell
unterstützt von
mugglebibliothek.de



Wer Interesse an der Unterstützung
dieser Website hat, melde sich
bitte bei
jasta72s@gmail.com
Willkommen bei einer
Stimme für das
Elektrische Universum
l
etzte Änderung: 11.12.2021

1. ENTFERNUNGEN IM WELTRAUM
1.1 ENTFERNUNGEN ZU DEN STERNEN
Wenn
wir
in
den
Nachthimmel
hinauf
schauen
und
all
die
Sterne
sehen,
von
denen
viele
Sonnen
sind,
die
unserer
eigenen
ähneln,
dann
scheinen
sie
eng
beieinander
zu
liegen.
Aber
sie
sind
einander
nicht
wirklich
nahe.
Das
Ausmaß
des
Raums zwischen ihnen ist riesig.
Entfernung
ist
eine
wichtige
und
schwierige
Quantität,
die
in
der
Astronomie
zu
messen
ist.
Wir
müssen
wissen,
wie
nah
wir
den
Sternen
und
Galaxien
sind,
weil
in
der
Astronomie
sehr
viel
von
der
Genauigkeit
dieser
Information
abhängt
̶̶
die
ausgestrahlte
Gesamtenergie
(Leuchtkraft),
die
Massen
von
orbitalen
Bewegungen,
die wahren Bewegunge
n der Sterne durch den Raum und ihre wahren Größen.
Das
neue
Bild des
Universums
2. Magnetische und Elektrische Felder
Sterne
sind
so
weit
entfernt,
dass
sie
selbst
in
Teleskopen
nur
winzige
Lichtpunkte
sind.
Ohne
Kenntnis
über
ihre
Entfernung
können
wir
nicht
genau
wissen,
ob
wir
auf
einen
kleinen,
aber
sehr
hellen
Stern
oder
auf
einen
größeren,
aber
weniger
hellen
Stern
sehen
oder
ob
dieser
Stern
oder
jener
Stern
uns
näher
ist.
Dies
trifft
auch
auf
Galaxien, Quasare, Jets und andere entfernte Phänomene zu.
Der
Abstand
zwischen
unseren
Augen
ermöglicht
uns
unsere
Tiefenwahrnehmung.
Jedes
Auge
muss
in
einem
bestimmten
Winkel
auf
einen
Gegenstand
sehen,
um
es
zu
zentrieren.
Das
Gehirn
interpretiert
diese
Winkel,
stellt
den
Fokus
des
Auges
ein,
gibt
uns
dadurch
ein
Gefühl
dafür,
wie
nahe
der
Gegenstand
ist
und
erschafft
die
Tiefenwahrnehmung
der
Welt
um
uns
herum.
Diese
biologische
Winkelbestimmung
ist
die
Grundlage
einer
Methode
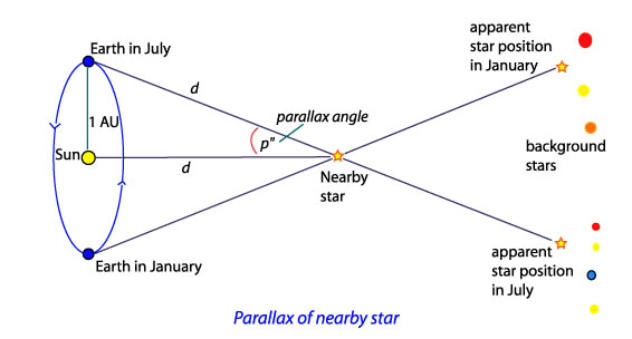
der Entfernungsbestimmung, die in der Astronomie Parallaxe genannt wird.
Triangulation
oder
trigonometrische
Parallaxe
ist
ein
direkter
Weg,
die
von
zwei
verschiedenen
Positionen
aus
gemessene
Winkeldifferenz
zu
verwenden,
um
die
Entfernung
zu
irgendeinem
Objekt
zu
ermitteln.
Durch
Beobachtung
der
Position
eines
Sterns
im
Vergleich
zu
einem
Stern
im
Hintergrund
von
der
entgegengesetzten
Seiten
unserer
Bahn
um
die
Sonne
aus
erhalten
wir
eine
Grundlinie.
Diese
ermöglicht
es
uns,
eine
Winkeldifferenz
aus
den
6
Monate
auseinander
liegenden
Beobachtungen
zu
bekommen,
welche
uns
in
die
Lage
versetzt,
die
Entfernung zu einem so entfernten Etwas wie einen Stern zu messen.
Sogar
mit
den
genaueren
Satellitendaten
von
Hipparcos
haben
Entfernungsmessungen
für
Sterne
bis
zu
einer
Entfernung
von
200-220
Lichtjahren
eine
Fehlerrate
bis
zu
10%
und
bis
zu
500
Lichtjahren
Entfernung
nimmt
die
Genauigkeit
weiter
ab.
Jenseits
dieser
Entfernung
sollten
Parallaxenmessungen
nicht
als
zuverlässig
angesehen
werden.
Pogge
behauptet
im
Link
zu
seiner
Lektion
5,
dass
Hipparcos’
Daten
“gute
Entfernungen
bis
zu
1000
Lichtjahren”
liefern
würden.
Doch
eine
geschätzte
Entfernung
von
nur
500
Lichtjahren
mit
±
20-30%
Fehler
ist
schon
viel
zu
ungenau,
um
von
Nutzen
zu
sein.
1000
Lichtjahre
sind
eine
fast
unbegreiflicher
Entfernung,
doch
nur
etwa
1%
des Weges durch unsere Milchstraßengalaxie.
Ein
Winkel
von
einem
Grad
wird
in
60
Bogenminuten
(60′)
unterteilt,
so
wie
laut
Übereinkunft
eine
Stunde
in
60
Minuten
unterteilt
wird.
Ebenso
kann
jede
Bogenminute
in
60
Bogensekunden
(60”)
unterteilt
werden.
Die
Parallaxe
zu
allen
Sternen
außer
unserer
Sonne
beträgt
weniger
als
eine
Bogensekunde.
Die
Parallaxe
zu
Alpha
Centauri
beträgt
tatsächlich
nur
etwa
0,75
Bogensekunden
oder
über
0,0002
Grad.
Der
Parallaxenwinkel
zu
allen
anderen
Sternen ist noch geringer als dieser kleine Wert.
Ein
Lichtjahr,
die
Entfernung,
welche
das
Licht
bei
seiner
Reise
durch
das
Vakuum
innerhalb
eines
Jahres
zurücklegt,
beträgt
etwa
9,6
Milliarden
Kilometer.
Wenn
man
3,26
Lichtjahre
durch
die
Parallaxe
zu
einem
Stern
in
Bogensekunden
teilt,
bekommt
man
die
Entfernung
zu
diesem
Stern,
gemessen
in
Lichtjahren.
Astronomen
bevorzugen
im
Allgemeinen
Parsec
(pc)
statt
Lichtjahre
für
Entfernungsmessungen,
obwohl
Parallaxen-messungen
nur verwendet werden können, um relativ kurze Entfernungen, wie die zu unserer Sonne, genau zu bestimmen.
Beispiel:
3,26
Lichtjahre
/
0,75
Bogensekunden
=
4,36
Lichtjahre
pro
Bogensekunde
(Lj/”),
das
sind
41,28
Billionen Kilometer oder 1,33 Parsec (Parallaxen pro Bogensekunde) zum nächsten Stern.
Beginnen wir zunächst nahe der Heimat.
1.2 MODELLIERUNG VON ENTFERNUNGEN IN UND NAHE UNSERES SONNENSYSTEMS
Robert Burnham entwickelte ein Modell, um uns in verständlichen Art und Weise zu zeigen, wie viel Raum dort draußen zwischen den Sternen liegt. Um seine Skala zu verstehen, müssen wir einige wirkliche Entfernungen kennen. Wie oben vermerkt beträgt die Entfernung von der Erde zur Sonne etwa 149,6 Millionen Kilometer. Normalerweise auf 150 Millionen Kilometer aufgerundet, wird dieser Abstand als Astronomische Einheit (AE, engl. AU) bezeichnet. Ein Lichtjahr (Lj) entspricht 63.294 AE. Zufälligerweise ist das ungefähr dieselbe Maßzahl wie eine Meile [1 Meile = 1.609 m] in Zoll [1 Zoll = 2,54 cm] entspricht, nämlich 63.360 Zoll. Deshalb gibt es etwa dieselbe Anzahl von Zoll in 1 AE (63.360 x 92.960.000) wie Meilen in 1 Lichtjahr (63.294 x 92.960.000). Das sind wirklich große Zahlen. Bleiben wir bei Zoll. Burnham setzte den Maßstab in seinem Modell so, dass 1 Zoll (1”) 1 AE entspricht oder 93 Millionen Meilen. Dann würde 1 Meile in unserem Modell 1 Lj entsprechen. Dieses Maß wäre 1:6.000.000.000.000. Diese eine Einheit würde sechs Millionen Millionen Einheiten repräsentieren, was ein Maßstab von eins zu 6 Billiarden oder 1:6×10¹² entspricht. Beginnen wir nun Burnhams Miniatur-Skalenmodell unseres Sonnensystems zu erklären. Wir wissen, dass die Entfernung von der Erde zur Sonne (1 AE) einem Zoll entspricht. Wie groß ist die Sonne? Der Durchmesser der Sonne ist ungefähr 870.000 Meilen, deshalb wird in unserem Skalenmodell die Sonne nur etwas unter 1/100 Zoll groß sein. Das ist ein sehr winziger Fleck. Die Erde wird einen Zoll von der Sonne entfernt sein, aber so klein (0,00009” oder 9 Einhunderttausendstel eines Zolls), dass wir nicht in der Lage wären, sie ohne ein Mikroskop zu sehen.
Das innere Sonnensystem, nicht maßstabsgerechte künstlerische Darstellung
Plutos
Bahnradius
ist
39,5
Mal
größer
als
der
der
Erde,
deshalb
befindet
sich
Pluto
39,5
Zoll
oder
fast
genau
1
Meter von der Sonne entfernt.
Die
Heliosphäre,
die
Region
um
die
Sonne
herum,
welche
der
Sonnenwind
durchdringt,
misst
7
Fuß
[2,13
m]
in unserem Modell.
Wo
befindet
sich
der
nächstgelegene
Stern
in
unserem
Modell?
Unser
nächster
Nachbar
ist
Alpha
Centauri,
über 4 Lichtjahre entfernt. Das sind mehr als 4 Meilen [6,436 m] in unserem Modell.
Ja,
4
Meilen.
Unsere
Sonne
ist
nur
ein
winziger
Fleck
und
es
sind
vier
Meilen
bis
zum
nächsten
Fleck.
Das
ist
eine
Menge
Raum
dazwischen.
Wie
groß
ist
aber
unsere
Galaxie
in
diesem
Modell?
Die
Modellgalaxie
würde
sich
über
100.000
Meilen
[160.900
km]
Durchmesser
erstrecken.
Der
schmale
Diskus
und
die
Spiralarme
wären
Tausende
Meilen
dick.
Ihre
zentrale
Verdickung
würde
von
oben
bis
unten
über
6000
Meilen
[9600
km]
messen.
Unsere
Galaxie
ist
aber
eine
von
Hunderten
von
Milliarden
von
Galaxien,
die
mit
unseren
gegenwärtigen
Messinstrumenten
im
beobachtbaren
Universum
sichtbar
sind.
Der
Nachthimmel
scheint
mit
Sternen
überfüllt
zu
sein,
doch
diese
sind
normalerweise
durch
Entfernungen
von
einander
getrennt,
die
dem
über
10
Millionenfachen
ihres
Durchmessers
entsprechen.
1.3 ENTFERNUNGEN UND GRAVITATION
Erinnert man sich daran, dass, wie Newton schrieb, die Gravitation mit der Entfernung zwischen zwei Objekten im Quadrat abnimmt (d.h. umgekehrt proportional zum Quadrat ist), dann ist die Anziehung der Schwerkraft zwischen den 4 Meilen auseinander liegenden zwei Flecken gar nicht so stark. Dasselbe gilt für die 4 Lichtjahre auseinander liegenden zwei Sterne. Verwenden wir nun die Newtonsche Gleichung, um herauszuarbeiten, wie groß sie tatsächlich ist. In der einfachen Gleichung unten, über der Arbeitstabelle, ist F die Kraft in Newton, G eine sehr kleine Zahl, die Gravitationskonstante genannt wird, M1 und M2 sind die geschätzten Massen der zwei Sterne in Kilogramm und r ist die Entfernung zwischen ihren Zentren in Metern. Astronomen verwenden das metrische oder SI-System, da es viel gebräuchlicher und praktischer ist als das traditionelle imperiale System mit Zoll, Fuß, Meilen, Pfund und Unze. Das Ergebnis der Berechnung, das unten unter der Abbildung gezeigt wird, basiert auf der Schwerkraft der Erde auf der Erdoberfläche, genannt “gee” (für “Gravitation”), ungeachtet des verwendeten Messsystems. F = G × (M1 × M2) ÷ R²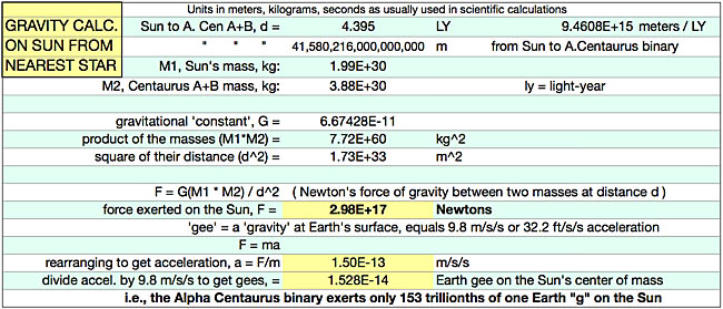
Berechnung der Gravitationskraft, die von Alpha Centauri auf die Sonne ausgeübt wird
Trotz
ihrer
großen
Massen
üben
die
zwei
Sterne
nur
eine
winzige
Anziehungskraft
aufeinander
aus.
Welche
Kräfte
auch
immer
das
Verhalten
der
Materie
im
Universum
beherrschen,
sie
müssen
stark
genug
und
in
der
Lage
sein, über diese immensen Entfernungen zu wirken.
Newtons
Gravitationsgesetz
hat
sich
beim
Erklären
von
Anziehungskräften
und
Umlaufbahnen
innerhalb
des
beschränkten
Bereichs
unseres
Sonnensystems
bewährt.
Doch
die
relativ
schwache
Schwerkraft
konnte
nur,
wenn
überhaupt,
über
interstellare
Entfernungen
wirksam
werden,
wenn
es
wahr
wäre,
dass
der
Weltraum
leer
ist
und
es
keine konkurrierenden Kräfte gäbe, die die Gravitation überwinden könnten.
Übersetzung H. Täger




Das neue Bild des Universums
2. Magnetische und Elektrische Felder



Sternentstehungsgebiet. Bildquelle: NASA/Hubble Space Telescope
Trigonometrisches Schema der Parallaxe.
Mit freundlicher Genehmigung der Australian Telescope Outreach and Education website
Die
Erde
ist
auf
einer
fast
kreisförmigen
Umlaufbahn
durchschnittlich
etwa
150
Millionen
Kilometer
von
der
Sonne
entfernt.
Diese
Entfernung
wird
in
der
Astronomie
oft
als
astronomische
Einheit
(AE)
[in
Englisch
AU]
bezeichnet.
Daher
beträgt
die
Entfernung
von
einer
Seite
der
Erdumlaufbahn
zur
Gegenseite
2
AE
oder
etwa
300
Millionen
Kilometer.
Wenn
wir
den
Winkel
zum
nächsten
Stern
(Alpha
Centauri)
von
einer
Seite
der
Umlaufbahn
messen,
dann
sechs
Monate
warten
und
wieder
messen,
stellen
wir
fest,
dass
die
Winkeldifferenz
ziemlich
klein
ist
und
eine
enorme
Messgenauigkeit
erfordert.
Beträgt
die
Parallaxe
eine
Bogensekunde
(1/3600
eines
Grades),
so
entspricht
das
einer
Entfernung
von
3,26
Lichtjahren.
Mehr
über
Parallaxen-
und
Entfernungsberechnungen
steht
bei
Pogge
und
hier
.
Die
Europäische
Weltraumorganisation
(European
Space
Agency,
Abk.
ESA)
startete
deshalb
ihr
automatisiertes
Satellitenteleskop
Hipparcos,
um
während
dessen
Betriebszeit
1989-1993
Messungen
an
über
118,000
Sternen
vorzunehmen.
Der
Auftrag
lautete:
Verbesserung
der
Genauigkeit
der
katalogisierten
Positionen
vieler
Sterne
und
Aktualisierung
der
Kataloge
Tycho
und
Tycho
2.
Von
den
neu
gemessenen
Parallaxen
erfüllten
20,870 Sterne das Kriterium, einen stellaren Parallaxenfehler von 10% oder weniger zu haben.
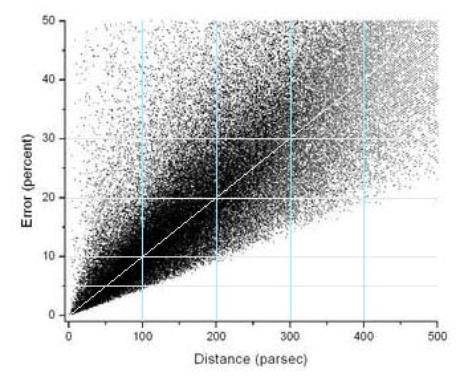
Darstellung von Parallaxenfehlern durch den Satelliten HIPPARCOS,
zusammengestellt durch Ralph Biggins aus Katalogdaten von ESA/HIPPARCOS.
Man beachte die mit wachsender Entfernung wachsenden prozentualen
Fehlergrenzen (der sich ausdehnende Keil).


- Vorwort
- Einführung
- 1. Abstände im Weltraum
- 2. Felder im Weltraum
- 3. Das Plasma
- 4. Der Elektromagnetismus
- 5. Stromfreie Doppelschichten u.a.
- 6. Ströme, Filamente und Pinche
- 7. Birkeland-Ströme und anderes
- 8. Stromschichen und -kreise
- 9. Instabilitäten
- 10. Rotationseffekte
- 11. Strahlung
- Elektrische Kometen
- Neues von Pluto
- Das Elektrische Sonnensystem
- Anhang1 - Vektoren
- Anhang2 - Maxwellsche Gleichung


- 1. Wo ist das Problem?
- 2. Wahre Wissenschaft
- 3. Wo bleibt die Mathematik?
- 4. Wo bleibt die Begutachtung?
- 5. Was ist mit der Gravitation?
- 6. Wie groß ist das Universum?
- 7. Wo ist der Leiter?
- 8. Ausbildungsdefizit?
- 9. Einstein widerlegt?
- 10. Warum Urknall bestreiten?
- 11. Was ist mit der Materie?
- 12. Elektrizität vor Magnetismus?















